Whats The Lcm Of 6 And 10
listenit
Mar 27, 2025 · 5 min read
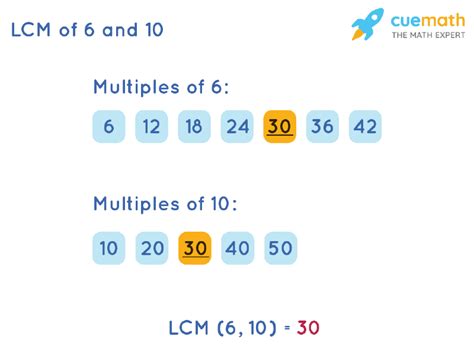
Table of Contents
What's the LCM of 6 and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the concept thoroughly opens doors to more complex mathematical operations and real-world applications. This comprehensive guide will not only answer the question, "What's the LCM of 6 and 10?" but also explore the underlying principles, different methods of calculation, and practical examples to solidify your understanding.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers in the set as factors. This concept is fundamental in various mathematical fields and has practical applications in areas like scheduling and measurement.
For instance, imagine you have two gears with 6 and 10 teeth respectively. The LCM helps determine how many rotations each gear needs to complete before they both return to their starting positions simultaneously. This seemingly simple problem highlights the real-world relevance of LCM.
Methods for Calculating the LCM
Several methods exist for calculating the LCM, each with its own advantages and suitability depending on the numbers involved. Let's explore the most common ones:
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. Simply list the multiples of each number until you find the smallest multiple common to both.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
Multiples of 10: 10, 20, 30, 40, 50, 60, ...
As you can see, the smallest multiple common to both 6 and 10 is 30. Therefore, the LCM of 6 and 10 is 30.
This method works well for small numbers but becomes cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 10: 2 x 5
Now, consider the prime factors involved: 2, 3, and 5. To find the LCM, take the highest power of each prime factor:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiply these highest powers together: 2 x 3 x 5 = 30
Therefore, the LCM of 6 and 10 using prime factorization is 30. This method is generally more efficient than listing multiples, particularly for larger numbers with many factors.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 6 and 10. The GCD is the largest number that divides both 6 and 10 without leaving a remainder. The GCD of 6 and 10 is 2.
Now, using the formula:
LCM(6, 10) x GCD(6, 10) = 6 x 10 LCM(6, 10) x 2 = 60 LCM(6, 10) = 60 / 2 = 30
This method requires calculating the GCD first, which can be done using various techniques like the Euclidean algorithm. This method provides an alternative approach, particularly useful when you already know the GCD.
Applications of LCM in Real Life
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 6 minutes, and the other every 10 minutes. The LCM (30 minutes) tells you how long you'll have to wait before both buses arrive simultaneously.
-
Construction and Engineering: In construction projects, materials often need to be cut into specific lengths. The LCM can help determine the most efficient cutting length to minimize waste. For example, if you need pieces of wood measuring 6 inches and 10 inches, cutting them into 30-inch lengths would ensure no waste.
-
Music: The LCM plays a crucial role in music theory, especially in determining the least common period of two or more musical notes.
-
Calendars: Calculating the next time certain events align, like the full moon and a specific day of the week, requires an understanding of LCM.
-
Manufacturing: Production lines often involve cycles of different durations. Determining when multiple lines coincide requires calculating the LCM.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all the prime factors from all the numbers and take the highest power of each. For the listing multiples method, it becomes even more cumbersome, highlighting the efficiency of the prime factorization approach for larger sets of numbers.
For example, let's find the LCM of 6, 10, and 15:
- Prime factorization of 6: 2 x 3
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
Highest power of 2: 2¹ = 2 Highest power of 3: 3¹ = 3 Highest power of 5: 5¹ = 5
LCM(6, 10, 15) = 2 x 3 x 5 = 30
Conclusion: Mastering LCM for Mathematical Proficiency
Understanding and calculating the least common multiple is a fundamental skill in mathematics with wide-ranging applications. While the simple listing method suffices for small numbers, the prime factorization method provides a more efficient and scalable solution, particularly when dealing with larger numbers or multiple integers. Mastering LCM not only strengthens your mathematical foundation but also equips you to tackle practical problems in various real-world scenarios. The ability to efficiently calculate LCM demonstrates a comprehensive understanding of number theory and its practical implications. By understanding the underlying principles and employing the most appropriate methods, you can confidently navigate problems involving LCM and appreciate its significance in diverse fields.
Latest Posts
Latest Posts
-
Lim As X Approaches Negative Infinity
Mar 30, 2025
-
How To Factor X 3 2x 2
Mar 30, 2025
-
What Is The Value Of 32 4
Mar 30, 2025
-
How Many Chromosomes Does A Mouse Have
Mar 30, 2025
-
How To Put Absolute Value In Ti 84
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Whats The Lcm Of 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
