What's In Between 1/4 And 3/8
listenit
May 11, 2025 · 5 min read
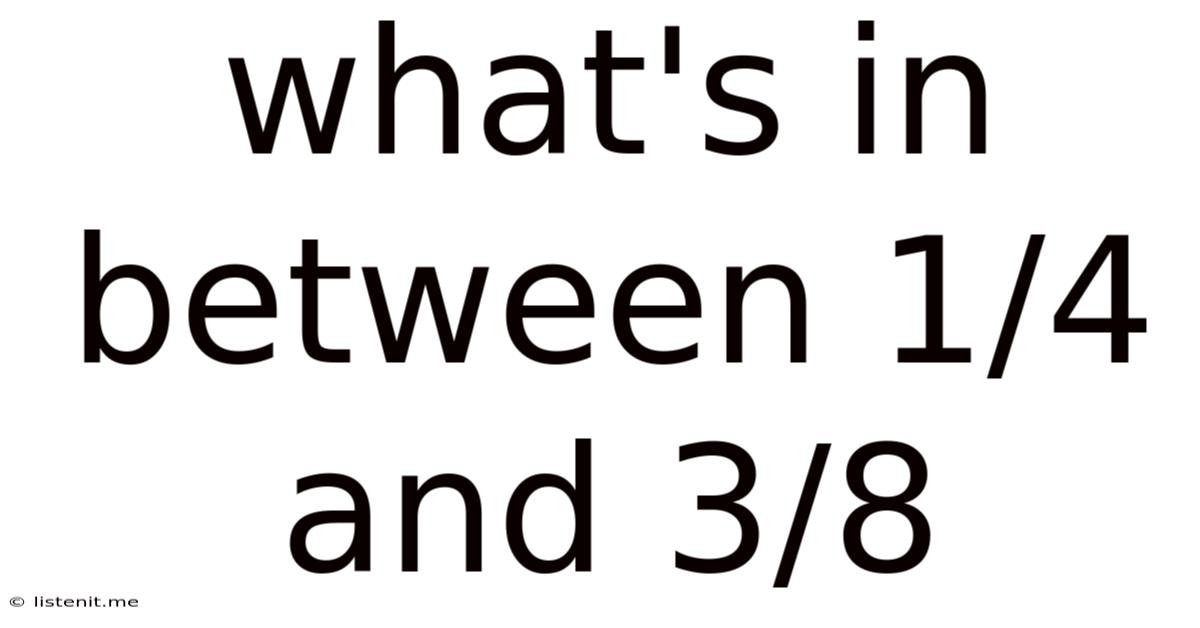
Table of Contents
What Lies Between 1/4 and 3/8? A Deep Dive into Fractions and Number Systems
This seemingly simple question, "What's in between 1/4 and 3/8?", opens a fascinating door into the world of mathematics, particularly fractions and the density of rational numbers. While the immediate answer might seem straightforward, exploring this question allows us to delve into fundamental mathematical concepts, explore various solution methods, and appreciate the rich tapestry of numbers that exist between any two given fractions.
Understanding Fractions: A Foundation
Before we tackle the problem directly, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two integers, the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
In our case, we have 1/4 and 3/8. 1/4 represents one out of four equal parts, while 3/8 represents three out of eight equal parts. To compare and work with these fractions effectively, we need a common denominator.
Finding a Common Denominator
The key to finding numbers between 1/4 and 3/8 lies in finding a common denominator. This allows us to express both fractions with the same denominator, making comparison and identification of intermediate values much easier.
The least common multiple (LCM) of 4 and 8 is 8. Therefore, we can rewrite 1/4 as an equivalent fraction with a denominator of 8:
1/4 = (1 × 2) / (4 × 2) = 2/8
Now we have 2/8 and 3/8. The numbers in between are easily identifiable as fractions with a denominator of 8 and numerators between 2 and 3. However, this is just the beginning.
Numbers Between 2/8 and 3/8: A Closer Look
At first glance, it might seem there are no numbers between 2/8 and 3/8. However, this is not true. The set of rational numbers (numbers that can be expressed as a fraction) is dense, meaning there are infinitely many rational numbers between any two distinct rational numbers.
We can find more numbers between 2/8 and 3/8 by increasing the denominator. For example, let's use a denominator of 16:
2/8 = (2 × 2) / (8 × 2) = 4/16
3/8 = (3 × 2) / (8 × 2) = 6/16
Now we can clearly see that 5/16 lies between 4/16 and 6/16.
We can continue this process indefinitely. By using larger and larger denominators, we can find an infinite number of fractions between 2/8 and 3/8. For instance, with a denominator of 32:
4/16 = 8/32
6/16 = 12/32
This reveals that 9/32, 10/32, and 11/32 are all between 2/8 and 3/8.
Exploring Decimal Representations
Another approach to finding numbers between 1/4 and 3/8 is to convert the fractions to decimals.
1/4 = 0.25
3/8 = 0.375
Now we can easily identify decimals between 0.25 and 0.375, such as:
- 0.26
- 0.27
- 0.28
- 0.29
- 0.30
- 0.31
- 0.32
- 0.33
- 0.34
- 0.35
- 0.36
- 0.37
While these decimals represent rational numbers, remember that many decimals are irrational, meaning they cannot be expressed as a fraction of two integers. These numbers also exist between 0.25 and 0.375, although they cannot be expressed precisely as fractions.
The Density of Rational Numbers: An Infinite Possibility
The key takeaway is the concept of the density of rational numbers. There are infinitely many rational numbers between any two distinct rational numbers. No matter how close two rational numbers are, we can always find another rational number between them. This property is fundamental to our understanding of the real number system.
This seemingly simple question has led us to explore the richness and complexity of the number system. We’ve used different methods to identify fractions and decimals between 1/4 and 3/8, highlighting the endless possibilities.
Beyond Fractions: Exploring Other Number Systems
While this discussion primarily focuses on fractions and decimals, it's worth noting that other number systems also exist, providing alternative ways to represent numbers between 1/4 and 3/8.
For instance, we could explore the concept of continued fractions, which offer a unique and elegant way to represent rational and irrational numbers. Or, we could delve into the realm of base-n number systems (where 'n' is the base, different from our usual base-10 system). Each of these systems offers a different perspective on the numbers residing between 1/4 and 3/8.
Practical Applications: Why This Matters
Understanding the density of rational numbers isn't just a theoretical exercise. It has significant practical applications in various fields:
-
Computer Science: Representing numbers in computers requires careful consideration of precision and the limitations of finite memory. Understanding the density of rational numbers helps in designing algorithms for numerical computations and data representation.
-
Engineering: In engineering designs, precision is crucial. The ability to find numbers between two given values helps engineers optimize designs and find solutions within specified tolerances.
-
Finance: Calculations involving interest rates, currency conversions, and stock prices often require dealing with fractions and decimals. An understanding of the number system helps in accurate financial modelling and analysis.
Conclusion: The Enduring Mystery of In-Between Numbers
The seemingly simple question of what lies between 1/4 and 3/8 has revealed a profound mathematical concept: the density of rational numbers. This density, the infinite possibility of numbers between any two given numbers, is a fundamental property of the real number system and has far-reaching implications in various fields. While we can find numerous fractions and decimals between these two fractions, the true beauty lies in the infinite possibilities that remain undiscovered, a testament to the endless richness and complexity of mathematics. The exploration continues...
Latest Posts
Latest Posts
-
English Scientist Who Coined The Term
May 12, 2025
-
A Pure Substance Made Of Only One Type Of Atom
May 12, 2025
-
Find Area Of A Parallelogram With Vertices
May 12, 2025
-
1 3 4 2 1 2
May 12, 2025
-
Has 5 Valence Electrons And Is In Period 3
May 12, 2025
Related Post
Thank you for visiting our website which covers about What's In Between 1/4 And 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.