What's 3 8 As A Percent
listenit
May 09, 2025 · 5 min read
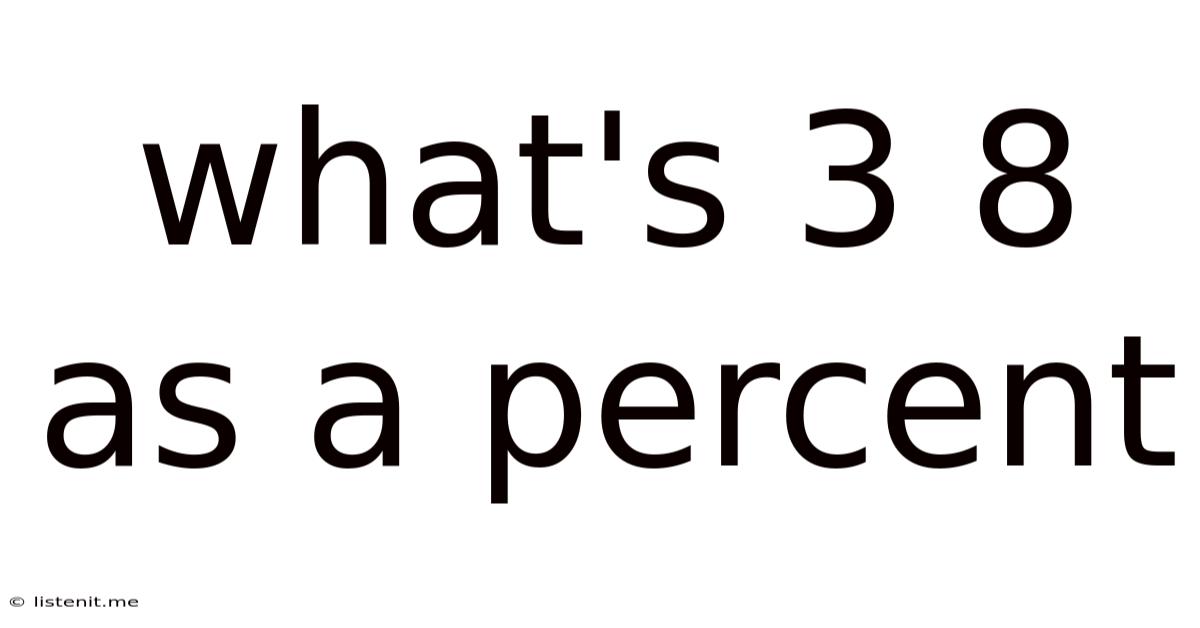
Table of Contents
What's 3/8 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistical data and financial reports. This comprehensive guide will walk you through the process of converting 3/8 to a percentage, explaining the underlying concepts and providing various methods to solve similar problems. We'll also explore the practical applications of this conversion and offer tips for mastering fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion of 3/8, let's refresh our understanding of fractions and percentages.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 parts out of a total of 8 equal parts.
Percentages: Expressing Parts per Hundred
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred." For instance, 50% means 50 out of 100, or 50/100. Percentages are widely used because they provide a standardized way to compare and understand proportions.
Converting 3/8 to a Percentage: Three Methods
There are several methods to convert the fraction 3/8 into a percentage. Let's explore three common approaches:
Method 1: Converting the Fraction to a Decimal then to a Percentage
This is arguably the most straightforward method. It involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (8). 3 ÷ 8 = 0.375
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol. 0.375 x 100 = 37.5%
Therefore, 3/8 is equal to 37.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This directly gives you the percentage because percentages are parts per hundred.
To do this, we need to find a number that, when multiplied by 8, gives us 100. However, 100 is not evenly divisible by 8. This means we'll get a decimal.
-
Find the equivalent decimal: We already know from Method 1 that 3/8 = 0.375
-
Express as a fraction over 100: We can express 0.375 as 375/1000.
-
Simplify to get percentage: To simplify to a fraction with a denominator of 100, we divide both numerator and denominator by 10. This gives us 37.5/100 which is 37.5%.
While this method is less direct than Method 1, it reinforces the concept of equivalent fractions and the meaning of percentage as parts per hundred.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage.
We can set up a proportion:
3/8 = x/100
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
8x = 300
x = 300 ÷ 8
x = 37.5
Therefore, 3/8 is equal to 37.5%.
This method demonstrates a powerful algebraic approach to solving similar problems, especially when dealing with more complex fractions.
Practical Applications of Converting Fractions to Percentages
Understanding fraction-to-percentage conversions is crucial in numerous real-world situations. Here are some examples:
-
Calculating discounts: If a store offers a 3/8 discount on an item, you can easily calculate the discount percentage as 37.5%.
-
Analyzing test scores: If you answered 3 out of 8 questions correctly on a quiz, your score is 37.5%.
-
Understanding statistical data: Many statistical reports use percentages to represent proportions. Converting fractions to percentages allows you to interpret these reports effectively.
-
Financial calculations: Percentages are essential in finance for calculating interest rates, returns on investments, and understanding financial statements.
-
Cooking and baking: Recipes often use fractions, but understanding the percentage equivalent can be helpful for scaling recipes up or down.
-
Everyday life: Calculating tips in restaurants, determining the percentage of a sale, or even understanding weather forecasts (e.g., 3/8 chance of rain) requires the ability to convert fractions to percentages.
Mastering Fraction-to-Percentage Conversions: Tips and Tricks
Here are some tips to help you master the art of converting fractions to percentages:
-
Practice regularly: The more you practice, the more comfortable you'll become with the process.
-
Use different methods: Try all three methods described above to find the one that works best for you.
-
Understand the underlying concepts: Make sure you understand the meaning of fractions and percentages before attempting conversions.
-
Use a calculator: A calculator can be a helpful tool, especially for more complex fractions.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Focus on simplifying fractions: Simplifying fractions before conversion can make the process easier.
-
Remember key conversions: Memorizing common fraction-to-percentage conversions (e.g., 1/2 = 50%, 1/4 = 25%, 3/4 = 75%) can speed up the process.
Conclusion: 3/8 as a Percentage and Beyond
We've thoroughly explored how to convert 3/8 to a percentage, demonstrating three different methods and highlighting the practical applications of this conversion. Mastering this skill is not just about solving mathematical problems; it's about developing a crucial skill that enhances your understanding of proportions and percentages in various aspects of life. By practicing regularly and understanding the underlying principles, you'll confidently convert fractions to percentages and apply this knowledge effectively in your daily life and professional endeavors. Remember, the key is practice and understanding the underlying concepts. So, grab a pencil and paper, and start practicing! You'll be surprised how quickly you can master this important skill.
Latest Posts
Latest Posts
-
Using Equations To Solve Word Problems
May 09, 2025
-
Does Pythagorean Theorem Work On All Right Triangles
May 09, 2025
-
What Is The Fraction For 0 32
May 09, 2025
-
25 Of What Number Is 35
May 09, 2025
-
How Many Electrons Are In A Neutral Carbon 14 Atom
May 09, 2025
Related Post
Thank you for visiting our website which covers about What's 3 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.