What's 20 Percent Of 30 Dollars
listenit
May 25, 2025 · 5 min read
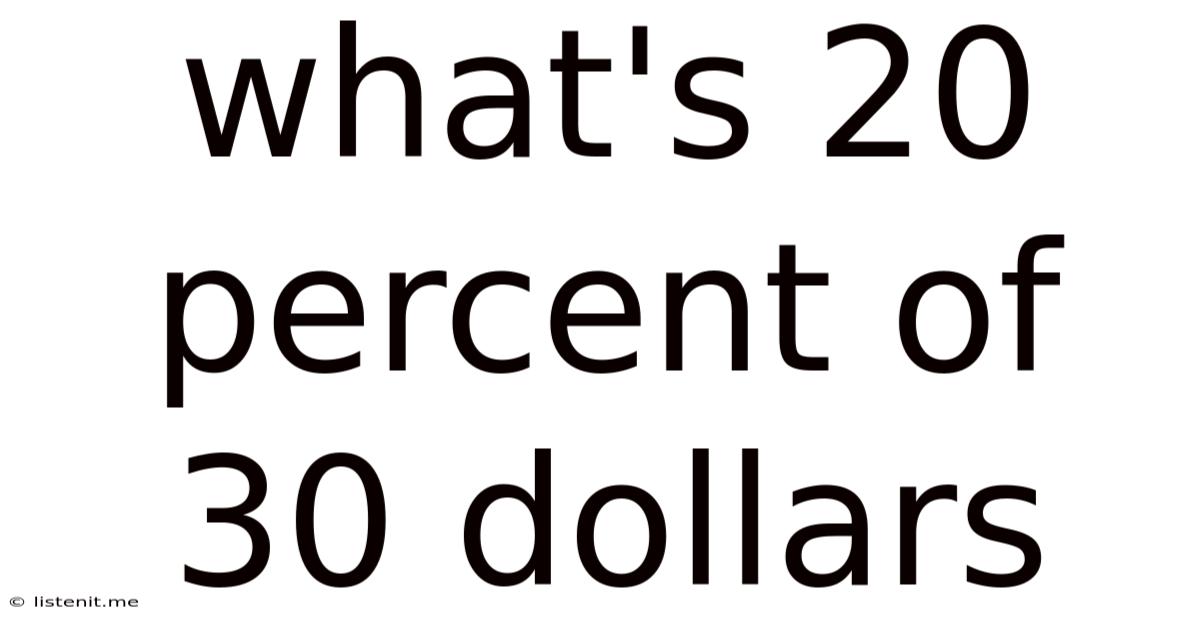
Table of Contents
What's 20 Percent of 30 Dollars? A Deep Dive into Percentages and Their Real-World Applications
This seemingly simple question, "What's 20 percent of 30 dollars?", opens the door to a world of mathematical concepts with far-reaching practical applications. While the answer itself is straightforward (6 dollars), understanding the how and why behind this calculation is crucial for navigating everyday finances, business decisions, and even advanced mathematical problems. This article delves into the calculation, explores various methods to solve it, and examines the broader implications of percentage calculations in various fields.
Understanding Percentages: The Building Blocks
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of one hundred". Therefore, 20% can be written as 20/100, or its simplified fraction, 1/5. This means 20% represents 20 parts out of every 100 parts.
This fundamental understanding is crucial because it allows us to convert percentages into decimals and fractions, which are often easier to work with in calculations. To convert a percentage to a decimal, simply divide the percentage by 100. For example, 20% becomes 0.20 (or 0.2). To convert a decimal to a percentage, multiply by 100 and add the "%" symbol.
Calculating 20% of 30 Dollars: Three Methods
Now, let's explore three different approaches to calculating 20% of 30 dollars:
Method 1: Using Decimal Multiplication
This is arguably the most straightforward method. We convert the percentage to a decimal and then multiply it by the total amount.
- Convert the percentage to a decimal: 20% = 0.20
- Multiply the decimal by the total amount: 0.20 * $30 = $6.00
Therefore, 20% of 30 dollars is $\boxed{$6}$.
Method 2: Using Fraction Multiplication
This method utilizes the fraction equivalent of the percentage.
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Multiply the fraction by the total amount: (1/5) * $30 = $6.00
Again, we arrive at the answer: $\boxed{$6}$.
Method 3: The Proportion Method
This method uses proportions to solve the problem. We set up a proportion where x represents the unknown value (20% of $30).
- Set up the proportion: 20/100 = x/$30
- Cross-multiply: 100x = 20 * $30
- Solve for x: 100x = $600 => x = $600/100 => x = $6
The result, once again, is $\boxed{$6}$.
Real-World Applications of Percentage Calculations
The ability to calculate percentages accurately is vital in numerous real-world situations. Here are some examples:
- Sales Tax: Calculating the sales tax on a purchase involves determining a percentage of the total cost.
- Discounts: Finding the final price after a discount requires calculating the percentage discount and subtracting it from the original price. For instance, a 20% discount on a $100 item would be a savings of $20, resulting in a final price of $80.
- Tips: Calculating a tip at a restaurant often involves determining a percentage of the bill. A 15% tip on a $50 meal would be $7.50.
- Interest Rates: Understanding interest rates on loans or savings accounts relies heavily on percentage calculations. A 5% interest rate on a $1000 loan means you'll pay $50 in interest per year.
- Profit Margins: Businesses use percentage calculations to determine their profit margins, which represent the percentage of revenue that is profit after deducting costs.
- Tax Calculations: Income tax, property tax, and other taxes are often calculated as percentages of income or property value.
- Investment Returns: Investors track the percentage return on their investments to gauge their success. A 10% return on a $5000 investment would be a gain of $500.
- Grade Calculations: Many academic grading systems use percentages to represent a student's performance on exams and assignments. A score of 85% on a test indicates a good understanding of the material.
Beyond the Basics: Advanced Percentage Applications
The principles of percentage calculations extend far beyond simple problems like finding 20% of 30 dollars. More complex scenarios might involve:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's a crucial concept in long-term investments and loan repayments.
- Percentage Change: This calculation determines the percentage increase or decrease between two values. For example, comparing sales figures from one year to the next would involve calculating the percentage change.
- Percentage Points: It's important to differentiate between percentage change and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
- Statistical Analysis: Percentages are fundamental in various statistical analyses, including probability, hypothesis testing, and data interpretation.
Mastering Percentages: Tips and Practice
To solidify your understanding of percentages and improve your calculation skills, consider the following:
- Practice regularly: Work through various percentage problems of increasing complexity. Start with simple problems and gradually move towards more challenging ones.
- Use different methods: Familiarize yourself with multiple methods for calculating percentages, such as decimal multiplication, fraction multiplication, and the proportion method. This will enhance your understanding and allow you to choose the most efficient approach for each problem.
- Utilize online resources: Numerous online calculators and educational websites offer practice problems and tutorials on percentage calculations.
- Relate it to real-life: Apply your knowledge of percentages to real-world situations. This will help you understand the practical implications of these calculations and make them more meaningful.
In conclusion, while the answer to "What's 20 percent of 30 dollars?" is a simple $6, the underlying principles and applications of percentage calculations are vast and essential for navigating the complexities of everyday life and various professional fields. By understanding the fundamentals and practicing regularly, you can build a strong foundation in this crucial mathematical concept. This allows you to confidently tackle more complex scenarios and make informed decisions in a wide range of contexts.
Latest Posts
Latest Posts
-
8 3 5 As An Improper Fraction
May 25, 2025
-
Greatest Common Factor Of 24 And 64
May 25, 2025
-
What Is The Greatest Common Factor For 9 And 27
May 25, 2025
-
What Is The Greatest Common Factor Of 60 And 84
May 25, 2025
-
Born In 1974 How Old Am I
May 25, 2025
Related Post
Thank you for visiting our website which covers about What's 20 Percent Of 30 Dollars . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.