What The Square Root Of 81
listenit
Apr 05, 2025 · 6 min read
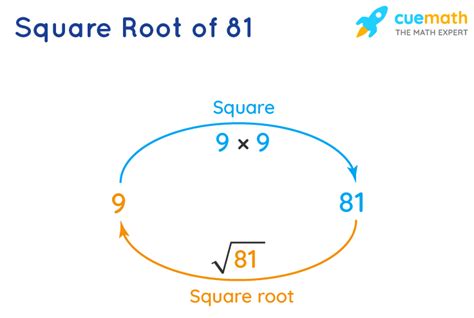
Table of Contents
What is the Square Root of 81? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 81?" opens a door to a fascinating world of mathematics, encompassing concepts far beyond basic arithmetic. While the answer itself is straightforward – 9 – understanding the underlying principles and the broader applications of square roots reveals a wealth of knowledge relevant to various fields. This article delves deep into the concept of square roots, exploring its history, calculation methods, practical applications, and its significance in advanced mathematical concepts.
Understanding Square Roots: The Basics
The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, it's the inverse operation of squaring a number. For example, since 9 multiplied by 9 (9²) equals 81, the square root of 81 (√81) is 9. This can be expressed mathematically as:
√81 = 9
This seemingly simple equation forms the foundation for countless mathematical operations and real-world applications.
Beyond the Basics: Positive and Negative Roots
It's crucial to understand that every positive number has two square roots: a positive and a negative root. While √81 = 9 is commonly accepted, it's equally true that (-9) * (-9) = 81. Therefore, a more complete answer would be ±9 (plus or minus 9). This concept is vital in higher-level mathematics, particularly when solving quadratic equations.
Visualizing Square Roots: The Geometric Perspective
Square roots have a strong geometric interpretation. Imagine a square with an area of 81 square units. The length of each side of this square is the square root of 81, which is 9 units. This geometric representation provides a visual and intuitive understanding of the concept, making it easier to grasp its meaning.
Methods for Calculating Square Roots
While the square root of 81 is relatively easy to determine, calculating the square root of other numbers can be more challenging. Several methods exist for finding square roots, ranging from simple estimation to complex algorithms:
1. Estimation and Mental Math
For perfect squares (numbers with whole-number square roots), estimation can be surprisingly effective. Knowing the squares of common numbers (e.g., 1²=1, 2²=4, 3²=9, and so on) allows for quick approximations. For numbers close to perfect squares, you can often deduce the approximate square root through logical reasoning.
2. Prime Factorization
For larger numbers, prime factorization can simplify the calculation. This method involves breaking down the number into its prime factors. For example, let's consider the square root of 144:
144 = 2 x 2 x 2 x 2 x 3 x 3 = 2⁴ x 3²
Therefore, √144 = √(2⁴ x 3²) = 2² x 3 = 4 x 3 = 12
3. The Babylonian Method (or Heron's Method)
This iterative method provides a precise approximation of square roots, even for non-perfect squares. It involves refining an initial guess through repeated calculations:
- Make an initial guess: Let's say we want to find the square root of 81. A reasonable guess is 9.
- Improve the guess: Divide the number by the guess (81/9 = 9).
- Average the guess and the result: Average the initial guess and the result from step 2 ((9+9)/2 = 9). This is a refined approximation of the square root.
- Repeat steps 2 and 3: Continue this process until the desired level of accuracy is achieved. In this case, we already obtained the exact answer in the first iteration because 81 is a perfect square.
4. Using a Calculator or Computer
Modern calculators and computer software readily provide the square root of any number. This is the most convenient method for quick and precise calculations.
Applications of Square Roots in Real Life
Square roots aren't just abstract mathematical concepts; they have significant practical applications across various fields:
1. Geometry and Engineering
As demonstrated earlier, square roots are fundamental to calculating areas and lengths in geometry. They're essential for solving problems related to right-angled triangles using the Pythagorean theorem (a² + b² = c²), which finds applications in construction, surveying, and navigation.
2. Physics and Science
Square roots play a critical role in many physics equations, including those dealing with velocity, acceleration, and energy. For instance, calculating the speed of an object involves square roots. They are also used extensively in other scientific disciplines, such as statistics and probability.
3. Finance and Investment
Square roots are utilized in financial calculations, particularly in determining standard deviation and variance in investment portfolios. These metrics help assess the risk associated with different investment strategies.
4. Computer Graphics and Game Development
Square roots are essential for calculating distances and positions in two and three-dimensional space, making them crucial for computer graphics, animation, and game development. They're used to determine the distance between points, essential for rendering and collision detection.
5. Signal Processing and Data Analysis
Square roots are employed in signal processing techniques such as the root mean square (RMS) calculation, which is used to measure the effective value of alternating currents and signals. In data analysis, they play a role in various statistical methods.
Square Roots in Advanced Mathematics
Beyond their practical applications, square roots are foundational to numerous advanced mathematical concepts:
1. Quadratic Equations
Solving quadratic equations (equations of the form ax² + bx + c = 0) often involves the use of the quadratic formula, which includes a square root. This formula provides the solutions for x, which can be real or complex numbers.
2. Complex Numbers
The concept of square roots extends into the realm of complex numbers, where the square root of a negative number is defined using the imaginary unit 'i', where i² = -1. This allows for solutions to equations that wouldn't be possible using only real numbers.
3. Calculus
Square roots appear in various calculus concepts, including derivatives and integrals. Understanding their properties is vital for solving problems related to rates of change and areas under curves.
4. Linear Algebra
Square roots are present in various matrix operations and eigenvalue problems in linear algebra. This branch of mathematics deals with systems of linear equations and their applications in diverse fields.
Conclusion: The Enduring Significance of Square Roots
The seemingly simple question of "What is the square root of 81?" has led us on a journey through the fascinating world of mathematics. While the answer – 9 – is straightforward, the underlying principles and applications of square roots are extensive and far-reaching. From their geometric interpretations to their roles in complex equations and advanced mathematical concepts, square roots are essential tools in various fields. Their importance extends beyond the classroom, impacting practical applications in engineering, physics, finance, and computer science. Understanding square roots is not just about solving a single equation; it's about grasping a fundamental concept that underpins a vast expanse of mathematical and scientific knowledge. This deep dive has aimed to enhance understanding and appreciation for this core mathematical concept.
Latest Posts
Latest Posts
-
The Horizontal Columns On The Periodic Table Are Called
Apr 05, 2025
-
What Is The Least Common Multiple Of 14 And 7
Apr 05, 2025
-
7 Cm Is How Many Inches
Apr 05, 2025
-
How Many Ounces Is A Fifth Of Liquor
Apr 05, 2025
-
Quadrilateral That Is Not A Rhombus
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What The Square Root Of 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
