What Percentage Is 5 Out Of 17
listenit
May 25, 2025 · 5 min read
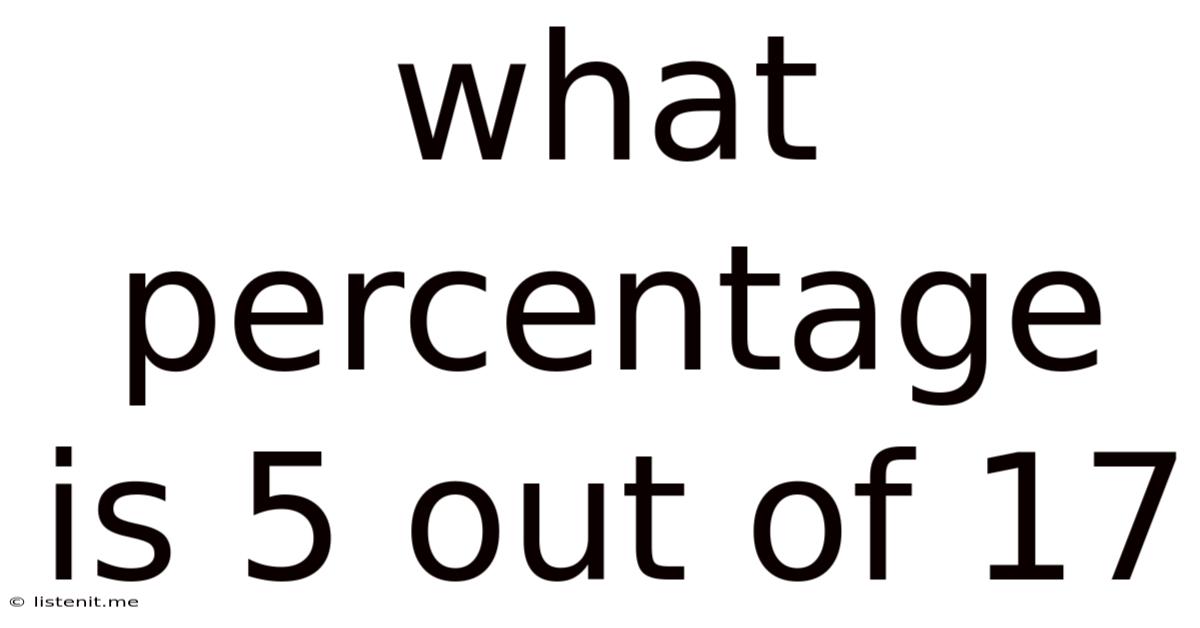
Table of Contents
What Percentage is 5 out of 17? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex statistical analysis. Understanding how to determine what percentage 5 represents out of 17 isn't just about finding a single answer; it's about grasping the underlying principles that allow you to tackle any similar percentage problem. This comprehensive guide will walk you through the calculation, explore different methods, and provide practical applications to solidify your understanding.
Understanding Percentages
Before diving into the specific calculation, let's review the basic concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Calculating the Percentage: 5 out of 17
The question "What percentage is 5 out of 17?" requires us to find the percentage that 5 represents when compared to the total of 17. We can use the following formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 5
- Whole: 17
Let's plug these values into the formula:
(5 / 17) * 100% = ≈ 29.41%
Therefore, 5 out of 17 is approximately 29.41%.
Different Methods for Calculating Percentages
While the above formula is the most straightforward, several alternative approaches can be used, each offering a slightly different perspective on percentage calculations.
Method 1: Using a Calculator
The simplest method is using a calculator. Simply divide 5 by 17 and then multiply the result by 100. Most calculators have a percentage function (%) that simplifies the process further.
Method 2: Long Division
For those who prefer a manual approach, long division provides a clear way to break down the calculation. Dividing 5 by 17 will give you a decimal value, which you can then convert to a percentage by multiplying by 100.
Method 3: Proportions
Another approach involves setting up a proportion. We know that 5 out of 17 is equivalent to 'x' out of 100. This can be represented as:
5/17 = x/100
To solve for x (the percentage), we cross-multiply:
17x = 500
x = 500 / 17
x ≈ 29.41
Method 4: Using Fractions
Expressing the problem as a fraction (5/17) offers another route to calculating the percentage. Convert the fraction to a decimal by performing the division, and then multiply the decimal by 100 to get the percentage.
Practical Applications of Percentage Calculations
Understanding percentage calculations isn't just an academic exercise. It's a vital skill with numerous real-world applications, including:
1. Financial Calculations:
- Interest rates: Calculating simple or compound interest relies heavily on percentages.
- Discounts: Determining the final price after a percentage discount requires understanding percentage reductions.
- Taxes: Calculating sales tax, income tax, or other taxes involves applying percentages to the base amount.
- Investment returns: Analyzing investment performance often involves calculating percentage gains or losses.
- Budgeting: Allocating funds based on percentages of your total income allows for effective financial planning.
2. Scientific and Statistical Analysis:
- Data representation: Percentages are frequently used to represent data in charts, graphs, and reports, making them easier to understand and interpret.
- Probability: Calculating probabilities involves expressing the likelihood of events as percentages.
- Experimental results: In scientific experiments, percentages are frequently used to express the success rate or variation within data sets.
3. Everyday Life:
- Sales and discounts: Determining how much you save during sales based on percentage discounts.
- Grading: Understanding your grade in a class often requires calculating your percentage score.
- Tip calculations: Determining an appropriate tip at a restaurant usually involves calculating a percentage of the bill.
- Surveys and polls: Results of surveys and polls are often reported using percentages to represent the opinions of a population sample.
Rounding and Precision
When working with percentages, rounding is often necessary. The result of (5/17) * 100 is approximately 29.4117647..., but for practical purposes, rounding to two decimal places (29.41%) is usually sufficient. The level of precision required depends on the context of the problem. For financial applications, greater precision might be needed, while for informal situations, rounding to the nearest whole number might suffice.
Error Analysis and Understanding Limitations
While percentage calculations are relatively straightforward, it's important to be aware of potential sources of error. Rounding errors can accumulate, especially when dealing with multiple calculations. Furthermore, when applying percentages to real-world scenarios, always consider the context and potential limitations. For instance, a percentage increase in sales might not accurately reflect the overall profitability of a business. Understanding these limitations is crucial for using percentages effectively and interpreting results accurately.
Advanced Percentage Calculations
While this guide has focused on basic percentage calculations, there are more complex scenarios that might require additional mathematical skills. These include:
- Calculating percentage change: This involves comparing two different values to determine the percentage increase or decrease.
- Calculating percentage points: This is distinct from percentage change and represents the absolute difference between two percentages.
- Compounding percentages: This applies when a percentage is applied repeatedly to an accumulating amount, as seen in compound interest calculations.
Mastering these advanced concepts will further expand your ability to use percentages in more sophisticated contexts.
Conclusion
Determining what percentage 5 represents out of 17, while seemingly simple, provides a springboard for understanding broader principles of percentage calculation. By exploring various methods and recognizing practical applications, you’ve equipped yourself with a valuable skill applicable across numerous fields. Remember to consider rounding, precision, and potential limitations when working with percentages in real-world contexts. With practice and a deeper understanding, you'll confidently navigate the world of percentages, empowering you to analyze data, make informed decisions, and interpret information effectively.
Latest Posts
Latest Posts
-
What Year Was I Born If Im 57
May 25, 2025
-
What Is 15 Percent Of 20 Dollars
May 25, 2025
-
Gcf Of 7 15 And 21
May 25, 2025
-
48 Years Old What Year Born
May 25, 2025
-
What Is The Gcf Of 17 And 51
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 5 Out Of 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.