What Percentage Is 30 Out Of 50
listenit
May 24, 2025 · 5 min read
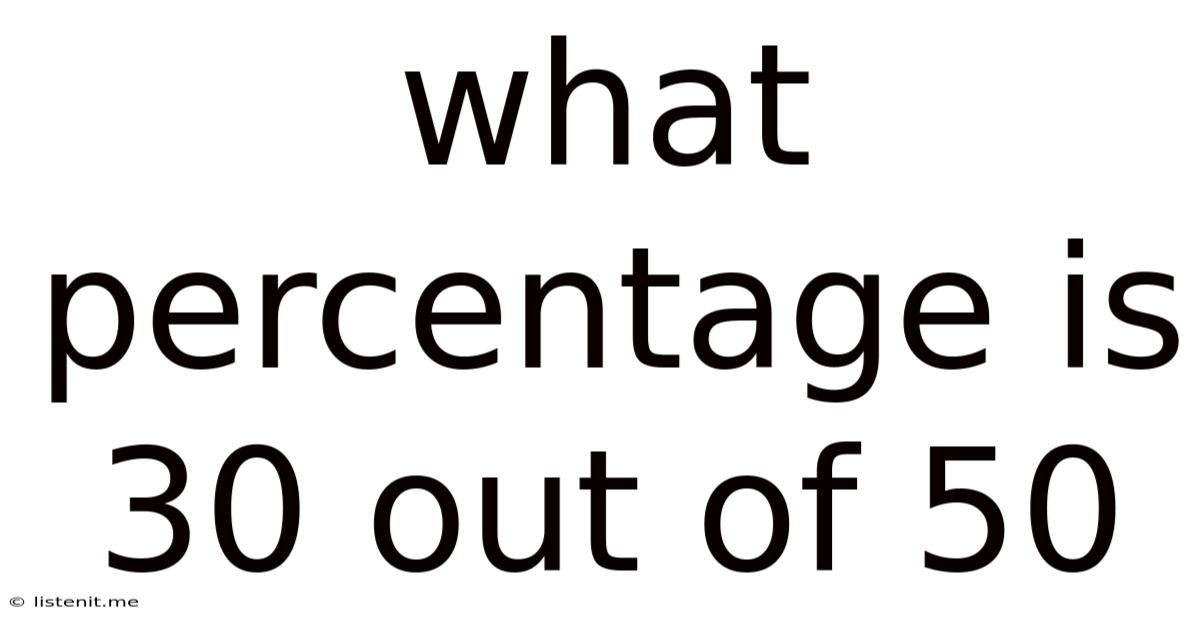
Table of Contents
What Percentage is 30 out of 50? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex statistical analysis. This comprehensive guide will not only answer the question, "What percentage is 30 out of 50?" but will also equip you with the knowledge and tools to calculate percentages confidently in various scenarios. We'll explore different methods, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Calculating the Percentage: The Basic Method
The most straightforward way to determine what percentage 30 is out of 50 involves a simple two-step process:
Step 1: Divide the part by the whole.
In this case, 30 is the "part" and 50 is the "whole." Therefore, we perform the calculation: 30 ÷ 50 = 0.6
Step 2: Multiply the result by 100 to express it as a percentage.
Taking the result from Step 1 (0.6) and multiplying it by 100 gives us: 0.6 x 100 = 60%
Therefore, 30 out of 50 is 60%.
Understanding the Concept of Percentages
A percentage represents a fraction of 100. It's a way to express a proportion or ratio as a part of a whole, where the whole is always considered 100%. Percentages are widely used because they provide a standardized and easily understandable way to compare different quantities. They're crucial in various areas, including:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Statistics: Representing data distributions, probabilities, and statistical significance.
- Science: Expressing concentrations, yields, and experimental results.
- Everyday Life: Understanding sales, tips, and comparisons of different products or services.
Alternative Methods for Percentage Calculation
While the basic method is efficient for simple calculations, understanding alternative methods provides flexibility and can be advantageous when dealing with more complex scenarios.
Using Proportions
Proportions offer a more formal approach to solving percentage problems. We can set up a proportion to find the percentage:
x/100 = 30/50
where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
50x = 3000
Then, we divide both sides by 50:
x = 3000/50 = 60
Therefore, x = 60%, confirming our earlier result.
Using a Calculator
Most calculators have a percentage function (%) that simplifies the process. You can input "30 ÷ 50 =" and then press the "%" button, which will directly give you the result: 60%. This method is particularly useful for quick calculations.
Practical Applications and Examples
Understanding percentage calculations extends far beyond simple arithmetic exercises. Let's explore some practical applications:
Example 1: Sales and Discounts
A store offers a 20% discount on an item originally priced at $50. To calculate the discount amount:
- Calculate the discount: 20% of $50 = (20/100) * $50 = $10
- Calculate the final price: $50 - $10 = $40
The final price after the 20% discount is $40.
Example 2: Grade Calculation
A student scores 45 out of 50 on a test. To determine the percentage score:
- Calculate the percentage: (45/50) * 100 = 90%
The student achieved a 90% score on the test.
Example 3: Tax Calculation
A purchase costs $100, and the sales tax is 6%. To calculate the total cost:
- Calculate the tax amount: 6% of $100 = (6/100) * $100 = $6
- Calculate the total cost: $100 + $6 = $106
The total cost including the 6% sales tax is $106.
Example 4: Interest Calculation
An investment of $1000 earns 5% interest annually. To calculate the interest earned after one year:
- Calculate the interest earned: 5% of $1000 = (5/100) * $1000 = $50
The investment earns $50 in interest after one year.
Beyond the Basics: Working with Percentages in Complex Scenarios
While the examples above showcase straightforward applications, percentage calculations can become more complex. Here are some advanced scenarios:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the difference between the values and expressing that difference as a percentage of the initial value.
-
Compound Interest: Compound interest involves calculating interest on both the principal amount and accumulated interest from previous periods. This requires iterative calculations.
-
Percentage Points vs. Percentages: It's crucial to differentiate between "percentage points" and "percentages." A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
-
Weighted Averages: When dealing with multiple percentages with different weights or contributions, weighted averages are necessary for an accurate overall percentage.
Troubleshooting Common Mistakes in Percentage Calculations
Several common errors can arise when working with percentages:
-
Incorrect order of operations: Always ensure you follow the correct order of operations (PEMDAS/BODMAS) to avoid errors in calculations.
-
Confusing percentage points and percentages: Clearly differentiate between these two concepts to avoid misinterpretations.
-
Rounding errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. Use enough decimal places during intermediate calculations to minimize inaccuracies in the final result.
-
Failing to convert fractions or decimals to percentages: Always convert fractions or decimals to percentages before interpreting results.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately is a highly valuable skill across various disciplines. This guide has provided a thorough explanation of calculating percentages, including various methods and practical applications. By understanding the fundamental concepts and avoiding common pitfalls, you can confidently tackle percentage problems in any context. Remember to practice regularly, and you’ll quickly master this essential mathematical skill. The more you practice, the more intuitive these calculations will become, allowing you to efficiently solve complex percentage problems and apply them in real-world situations. Don't hesitate to revisit this guide and use the examples provided as you practice and continue your journey to mastering percentage calculations.
Latest Posts
Latest Posts
-
What Is The Gcf Of 8 And 5
May 24, 2025
-
Greatest Common Factor Of 3 And 12
May 24, 2025
-
What Was The Date Of Last Friday
May 24, 2025
-
Find The Greatest Common Factor Of 16 27 And 20
May 24, 2025
-
What Is 8 Out Of 10 As A Percentage
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 30 Out Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.