What Percentage Is 30 Out Of 200
listenit
May 25, 2025 · 5 min read
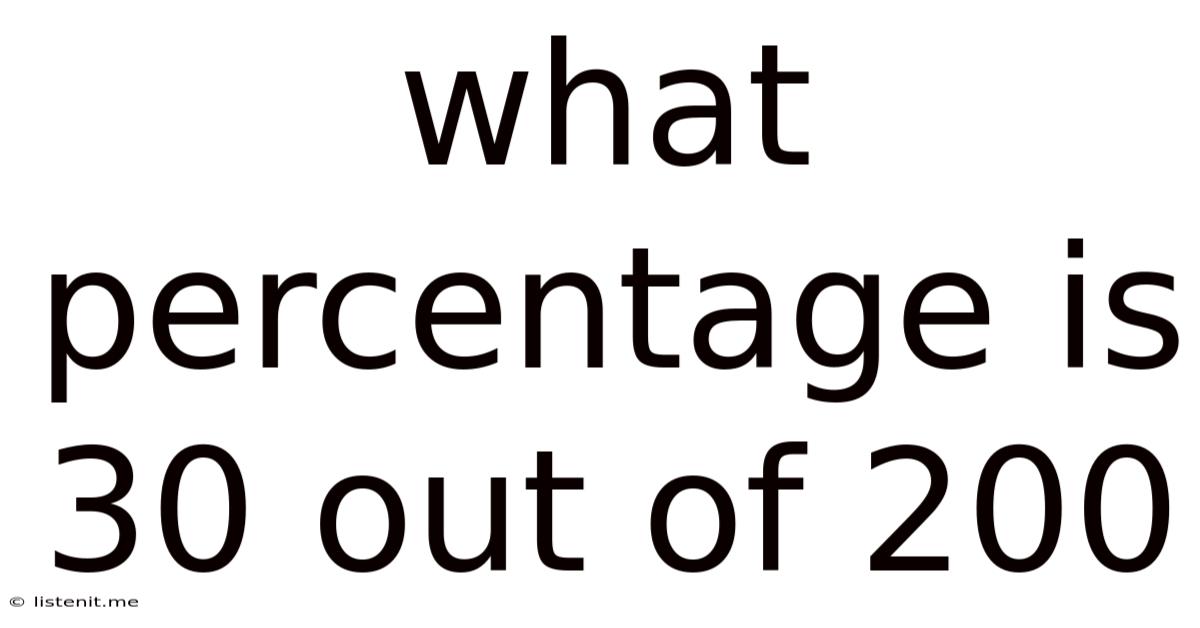
Table of Contents
What Percentage is 30 out of 200? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This article delves into the intricacies of calculating percentages, using the example of "What percentage is 30 out of 200?" as a springboard to explore various methods and applications.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" originates from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Understanding this foundational concept is key to tackling percentage calculations. Whether you're calculating discounts, interest rates, or statistical probabilities, the underlying principle remains consistent: expressing a proportion as a fraction of 100.
Method 1: The Formulaic Approach
The most straightforward method for determining what percentage 30 represents of 200 involves a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 30 (the number we're interested in expressing as a percentage)
- Whole: 200 (the total number)
Substituting these values into the formula:
(30 / 200) * 100 = 15%
Therefore, 30 is 15% of 200.
This formula provides a clear and concise way to calculate percentages and is readily adaptable to various scenarios.
Method 2: Using Decimal Equivalents
Another approach involves converting the fraction to a decimal and then multiplying by 100. This method offers a slightly different perspective on the calculation:
- Form the fraction: 30/200
- Simplify the fraction (optional but helpful): This fraction simplifies to 3/20. Simplifying often makes the next step easier.
- Convert the fraction to a decimal: Divide the numerator (3) by the denominator (20). 3 ÷ 20 = 0.15
- Multiply by 100 to express as a percentage: 0.15 * 100 = 15%
This method highlights the connection between fractions, decimals, and percentages, reinforcing the underlying mathematical principles.
Method 3: Proportion and Cross-Multiplication
This method uses the concept of proportions, setting up an equation with two equivalent ratios:
- x/100 = 30/200
Where 'x' represents the percentage we are trying to find. We can solve for 'x' using cross-multiplication:
- 200x = 3000
- x = 3000 / 200
- x = 15
Therefore, x = 15%, confirming our previous results. This method is particularly useful when dealing with more complex percentage problems.
Practical Applications: Real-World Examples
Understanding percentage calculations extends far beyond simple mathematical exercises. Let's explore some real-world applications:
1. Sales and Discounts:
Imagine a store offering a discount of 30 dollars off an item originally priced at 200 dollars. Using our percentage calculation, we can determine that the discount is 15% (30/200 * 100 = 15%). This allows customers to quickly understand the value of the discount.
2. Financial Analysis:
Investors often use percentages to analyze investment performance. If an investment of 200 dollars yields a profit of 30 dollars, the return on investment (ROI) is 15%. This information is crucial for comparing investment options and making strategic decisions.
3. Test Scores and Grades:
In education, percentages are widely used to represent student performance. If a student answers 30 questions correctly out of a total of 200 questions, their score is 15%. This allows for a standardized way to assess student understanding.
4. Statistics and Data Analysis:
Percentages are indispensable tools in statistical analysis. They allow researchers to express proportions within datasets, facilitating comparisons and the identification of trends. For example, if 30 out of 200 surveyed individuals prefer a particular product, this represents 15% preference.
Advanced Percentage Calculations: Beyond the Basics
While calculating "what percentage is 30 out of 200" is relatively straightforward, more complex scenarios might require slightly different approaches:
1. Finding the Whole when Given the Percentage and Part:
Suppose we know that 15% of a number is 30. To find the whole number, we can set up an equation:
0.15 * x = 30
Solving for x:
x = 30 / 0.15 = 200
2. Finding the Part when Given the Percentage and Whole:
If we know that 15% of 200 is a certain number, we can find that number by multiplying the percentage (as a decimal) by the whole:
0.15 * 200 = 30
3. Percentage Increase or Decrease:
Calculating percentage changes involves comparing two numbers. For example, if a value increases from 200 to 230, the percentage increase is calculated as:
((230 - 200) / 200) * 100 = 15%
Similarly, if a value decreases from 200 to 170, the percentage decrease is:
((200 - 170) / 200) * 100 = 15%
Tips for Accurate Percentage Calculations
- Double-check your work: Errors in calculation can lead to incorrect conclusions. Always review your steps to ensure accuracy.
- Use a calculator when necessary: For complex calculations or when dealing with large numbers, a calculator can help improve speed and accuracy.
- Understand the context: The meaning of a percentage depends heavily on the context. Always consider the context when interpreting results.
- Round appropriately: Depending on the context, rounding your final percentage to a certain number of decimal places might be necessary.
Conclusion: Mastering Percentage Calculations
The seemingly simple question "What percentage is 30 out of 200?" unveils a world of practical applications for percentage calculations. Mastering these calculations is crucial for success in various fields, from personal finance to advanced statistical analysis. By understanding the different methods and applying them to real-world scenarios, you can effectively utilize percentages to analyze data, make informed decisions, and solve problems efficiently. Remember to always double-check your work and consider the context of your calculations to ensure accuracy and meaningful interpretation of results. With practice and understanding, percentage calculations will become an intuitive and essential part of your problem-solving toolkit.
Latest Posts
Latest Posts
-
Least Common Multiple Of 21 And 24
May 25, 2025
-
How Do You Find Out 40 Percent Of A Number
May 25, 2025
-
What Is The Gcf Of 12 And 72
May 25, 2025
-
Greatest Common Factor Of 24 And 45
May 25, 2025
-
What Is The Gcf Of 18 And 32
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 30 Out Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.