What Percentage Is 25 Of 35
listenit
May 21, 2025 · 5 min read
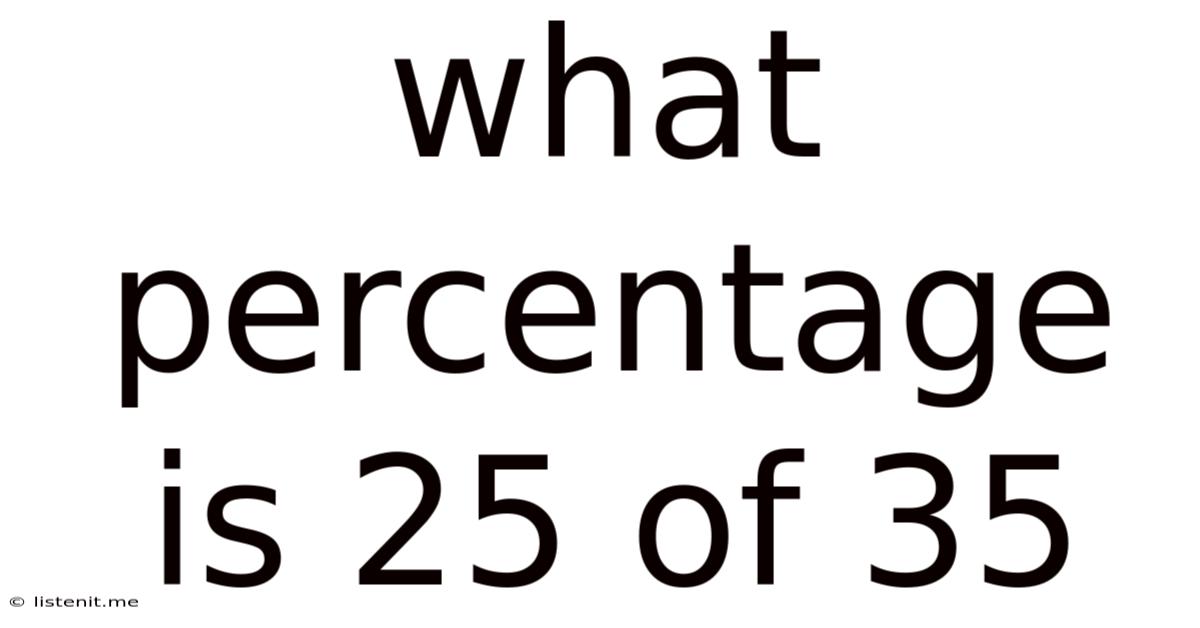
Table of Contents
What Percentage is 25 of 35? A Comprehensive Guide to Percentage Calculations
Determining what percentage 25 represents of 35 might seem like a simple arithmetic problem, but understanding the underlying principles of percentage calculations is crucial for various applications in daily life, academics, and professional fields. This comprehensive guide will not only answer the question but also delve into the methods, applications, and significance of percentage calculations. We'll explore different approaches, explain the concepts clearly, and provide examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentages is "%". Percentages are a versatile tool used to represent proportions, ratios, and changes in quantities. They provide a standardized way to compare different values, making them easier to understand and interpret.
Calculating "What Percentage is 25 of 35?"
There are several ways to calculate what percentage 25 represents of 35. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 25
- Whole: 35
Applying the formula:
(25 / 35) x 100% = 71.42857%
Therefore, 25 is approximately 71.43% of 35.
Method 2: Using Decimal Equivalents
We can also solve this by first converting the fraction to a decimal and then multiplying by 100%:
- Divide the part by the whole: 25 / 35 = 0.7142857
- Multiply the decimal by 100%: 0.7142857 x 100% = 71.42857%
- Round to the desired number of decimal places: 71.43%
This method provides the same result as the formula method.
Method 3: Using Proportions
We can set up a proportion to solve for the percentage:
25/35 = x/100
Cross-multiplying:
35x = 2500
Solving for x:
x = 2500 / 35 = 71.42857
Therefore, x ≈ 71.43%, confirming our previous calculations.
Practical Applications of Percentage Calculations
Percentage calculations are incredibly versatile and are used in a wide range of situations, including:
1. Finance and Business:
- Calculating Profit Margins: Businesses use percentages to determine their profit margins by comparing profits to revenue.
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Discounts and Sales: Retailers advertise discounts as percentages to attract customers.
- Tax Calculations: Governments use percentages to calculate various taxes, such as income tax, sales tax, and VAT.
- Investment Returns: Investors use percentages to track the returns on their investments.
2. Academics and Science:
- Grade Calculation: Grades in many educational systems are expressed as percentages.
- Statistical Analysis: Percentages are fundamental in statistical analysis to represent proportions and probabilities.
- Scientific Research: Percentages are used extensively in scientific research to present data and analyze results.
- Data Representation: Charts and graphs often use percentages to visually represent data proportions.
3. Everyday Life:
- Shopping: Comparing prices and discounts involves percentage calculations.
- Cooking: Recipes often provide ingredient amounts as percentages of the total.
- Tipping: Calculating tips in restaurants usually involves percentages.
- Understanding Surveys and Polls: Percentages are used to represent the results of surveys and polls.
Beyond the Basics: Advanced Percentage Calculations
While calculating "what percentage is 25 of 35" provides a foundational understanding, let's explore some more complex scenarios:
1. Percentage Increase and Decrease:
Calculating percentage changes (increases or decreases) requires a slightly different approach. The formula is:
[(New Value - Old Value) / Old Value] x 100% = Percentage Change
For example, if a value increases from 50 to 60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
2. Finding the Original Value:
Sometimes you know the percentage and the final value, but need to find the original value. For instance, if a price after a 10% discount is $90, you can calculate the original price:
Let x be the original price.
x - 0.10x = $90 0.90x = $90 x = $90 / 0.90 = $100
The original price was $100.
3. Compound Percentages:
Compound percentages involve applying a percentage change multiple times. For example, if you invest $1000 with a 5% annual interest rate compounded annually, after two years you'll have:
Year 1: $1000 x 1.05 = $1050 Year 2: $1050 x 1.05 = $1102.50
This is different from a simple 10% increase (which would be $1100).
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The key to mastering percentage calculations is consistent practice. Solve various problems to build your confidence and understanding.
- Use a Calculator: Calculators can be extremely helpful, particularly for more complex calculations.
- Understand the Concept: Focus on understanding the underlying principle of percentages as a fraction of 100.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Learn Different Methods: Familiarize yourself with multiple methods for calculating percentages to choose the most efficient approach for each problem.
- Utilize Online Resources: Numerous websites and apps offer practice problems and tutorials on percentage calculations.
Conclusion: The Power of Percentages
The ability to perform percentage calculations accurately and efficiently is an essential skill for success in many areas of life. Understanding the fundamental concepts and mastering different calculation methods will empower you to handle various quantitative tasks effectively. From simple everyday calculations to complex financial analyses, the versatility and importance of percentages cannot be overstated. By consistently practicing and applying the knowledge gained from this guide, you'll develop a strong understanding of percentages and confidently tackle any percentage-related problem you encounter. Remember to always check your answers and use a calculator when necessary to minimize errors. The journey to mastering percentages is a valuable investment in your overall problem-solving capabilities.
Latest Posts
Latest Posts
-
Nursing Care End Stage Liver Disease
Jun 05, 2025
-
Why Is Dlco Increased In Asthma
Jun 05, 2025
-
When To Use A Multiple Regression Analysis
Jun 05, 2025
-
Organisms That Live In The Hadal Zone
Jun 05, 2025
-
How Does The Immune System Work With The Skeletal System
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 25 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.