What Percent Of 50 Is 23
listenit
May 26, 2025 · 5 min read
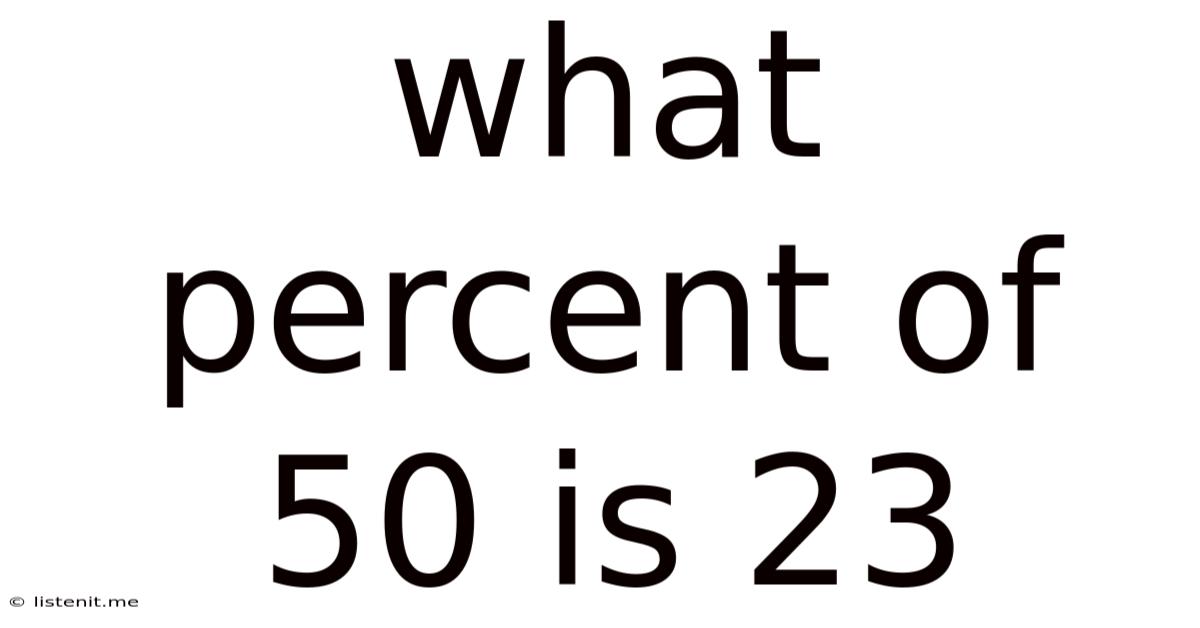
Table of Contents
What Percent of 50 is 23? A Deep Dive into Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. This article will comprehensively explore how to calculate what percentage 23 represents of 50, providing step-by-step explanations, practical examples, and related concepts to solidify your understanding. We'll also delve into the broader context of percentage calculations and their importance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Therefore, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Percentages are incredibly useful because they provide a standardized way to compare proportions. Whether you're comparing sales figures, test scores, or the composition of a mixture, percentages allow for easy and intuitive understanding.
Calculating the Percentage: Step-by-Step
To determine what percentage 23 is of 50, we follow these steps:
Step 1: Set up the Proportion
We can represent the problem as a proportion:
23/50 = x/100
Where 'x' represents the percentage we want to find.
Step 2: Solve for x
To solve for 'x', we can cross-multiply:
50x = 23 * 100
50x = 2300
x = 2300 / 50
x = 46
Step 3: State the Answer
Therefore, 23 is 46% of 50.
Alternative Method: Using Decimal Conversion
Another way to solve this problem is by using decimal conversion:
Step 1: Convert the Fraction to a Decimal
Divide 23 by 50:
23 ÷ 50 = 0.46
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100:
0.46 * 100 = 46%
This method offers a more direct route to the solution and is often preferred for its simplicity.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. Understanding percentage change is vital for tracking financial performance.
-
Statistics: Percentages are essential for representing data in a clear and concise manner. They are used extensively in surveys, polls, and data analysis to illustrate proportions and trends.
-
Science: In chemistry, percentages are used to express concentrations of solutions. In biology, percentages might represent the success rate of an experiment or the proportion of a population with a specific trait.
-
Retail: Discounts are usually expressed as percentages, making it easy for customers to understand the price reduction. Sales tax is also calculated as a percentage of the purchase price.
-
Everyday Life: Calculating tips in restaurants, figuring out the percentage of a sale, and understanding nutritional information on food labels all involve percentage calculations.
Beyond the Basics: Percentage Increase and Decrease
Understanding percentage calculations extends beyond simply finding what percentage one number is of another. Two crucial concepts are percentage increase and percentage decrease.
Percentage Increase: This represents the relative increase in a quantity expressed as a percentage. The formula is:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100
Percentage Decrease: This represents the relative decrease in a quantity expressed as a percentage. The formula is:
Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
For example, if a product's price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100 = 20%
Advanced Percentage Problems and Applications
While the problem of finding what percentage 23 is of 50 is relatively straightforward, more complex percentage problems can arise. These often involve multiple steps or require a deeper understanding of proportional reasoning. For example:
-
Finding the original value: If a product is discounted by 20% and now costs $40, what was the original price?
-
Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires iterative percentage calculations.
-
Analyzing statistical data: Interpreting percentages within larger datasets requires a solid understanding of statistical concepts and methods.
Mastering basic percentage calculations provides the foundation for tackling these more advanced problems and confidently applying percentage calculations in various contexts.
Error Handling and Common Mistakes
When working with percentages, several common errors can occur:
-
Incorrectly setting up the proportion: Ensure the correct values are placed in the numerator and denominator of the fraction.
-
Misinterpreting the question: Carefully read the problem statement to understand what is being asked.
-
Calculation errors: Double-check your arithmetic to avoid simple mistakes.
-
Using the wrong formula: Ensure you are using the appropriate formula for the type of percentage problem you are solving.
Improving your Percentage Calculation Skills
To improve your proficiency in percentage calculations, consider these tips:
-
Practice regularly: The more you practice, the more comfortable you will become with the concepts and calculations.
-
Use different methods: Experiment with different approaches to solving percentage problems, such as the proportion method and the decimal conversion method.
-
Understand the underlying concepts: A strong understanding of fractions, decimals, and ratios will significantly improve your ability to work with percentages.
-
Seek help when needed: Don't hesitate to ask for help if you are struggling with a particular problem. There are many resources available online and in textbooks that can provide assistance.
-
Utilize online calculators (for verification only): While calculators can be helpful for checking your answers, it's crucial to understand the underlying process. Relying solely on calculators without grasping the concepts can hinder your learning.
Conclusion: The Importance of Mastering Percentages
Understanding percentages is a vital skill for navigating various aspects of life, from managing personal finances to interpreting data and solving complex problems in various fields. By mastering the fundamental concepts and practicing regularly, you can build a strong foundation for tackling even the most challenging percentage-related calculations. This article has provided a comprehensive guide, covering basic calculations, advanced applications, and strategies for improving your skills. Remember that consistent practice and a solid grasp of the underlying principles are key to mastering this essential mathematical concept. The ability to confidently handle percentage calculations will undoubtedly enhance your problem-solving skills and provide valuable tools for success in many areas of life.
Latest Posts
Latest Posts
-
How Many Hours Is In 10 Days
May 26, 2025
-
How To Find The Measurements Of A Triangle
May 26, 2025
-
25 Is 80 Of What Number
May 26, 2025
-
What Is 10 Factors Of 3
May 26, 2025
-
5 Divided By 4 5 As A Fraction
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.