What Percent Of 5 Is 2
listenit
May 23, 2025 · 5 min read
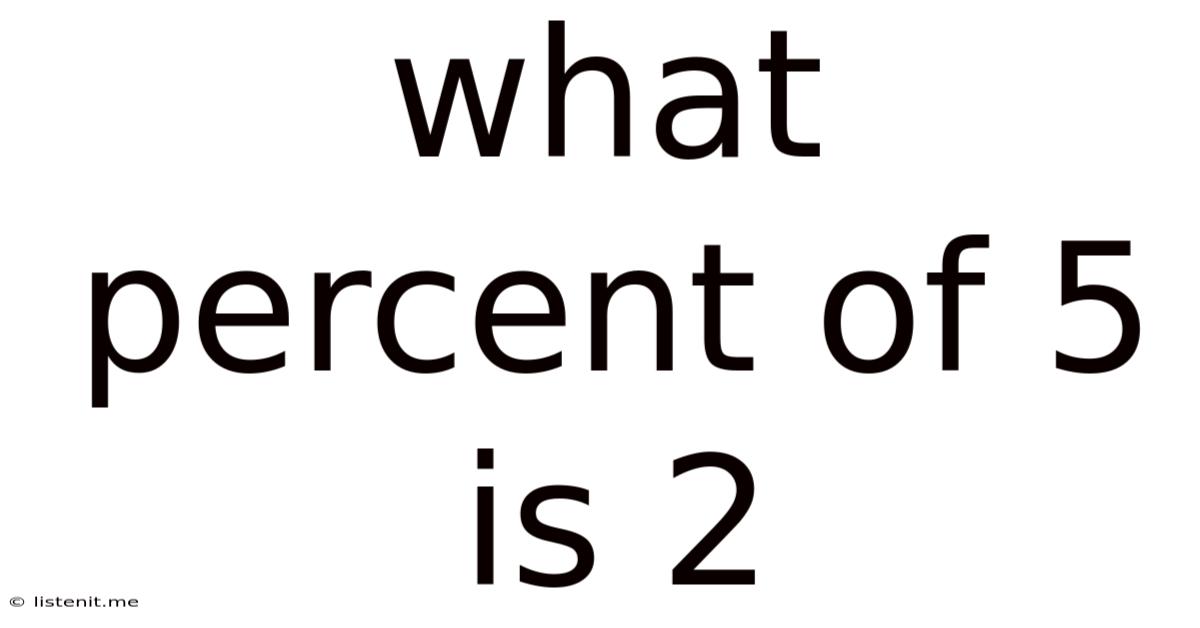
Table of Contents
What Percent of 5 is 2? A Deep Dive into Percentage Calculations
The question, "What percent of 5 is 2?" might seem simple at first glance. It's a fundamental concept in mathematics, crucial for understanding percentages in various real-world applications, from calculating discounts and taxes to understanding statistics and financial reports. This article will delve into not only how to solve this specific problem but also explore the underlying principles of percentage calculations, providing you with a comprehensive understanding and the tools to tackle similar problems with ease.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred," indicating a ratio to 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Understanding the relationship between fractions, decimals, and percentages is fundamental. They are all different ways of representing the same proportion. Let's illustrate this:
- Fraction: 2/5 represents two parts out of five.
- Decimal: Dividing 2 by 5 gives us 0.4.
- Percentage: To convert the decimal 0.4 to a percentage, we multiply it by 100: 0.4 * 100 = 40%.
Therefore, 2/5 = 0.4 = 40%.
Solving "What Percent of 5 is 2?"
Now let's tackle the problem directly: "What percent of 5 is 2?" We can approach this using several methods:
Method 1: Using Proportions
Proportions are a powerful tool for solving percentage problems. We can set up a proportion to represent the problem:
x/100 = 2/5
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
5x = 200
Then, divide both sides by 5:
x = 40
Therefore, 2 is 40% of 5.
Method 2: Using the Formula
The formula for calculating percentages is:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 2
- Whole: 5
Substituting these values into the formula:
Percentage = (2 / 5) * 100 = 0.4 * 100 = 40%
Again, we find that 2 is 40% of 5.
Method 3: Working with Decimals
We can also approach this by first finding the decimal equivalent of the fraction 2/5, which is 0.4. Then, multiplying by 100 gives us the percentage:
0.4 * 100 = 40%
This method highlights the direct relationship between decimals and percentages.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous everyday situations:
1. Shopping and Sales:
Discounts are often expressed as percentages. If a store offers a 20% discount on a $50 item, you can calculate the discount amount and the final price using percentage calculations.
2. Finance and Investments:
Interest rates on loans and savings accounts are expressed as percentages. Calculating interest earned or paid requires a thorough understanding of percentage calculations. Understanding percentage changes in investment values is crucial for tracking portfolio performance.
3. Taxes:
Sales tax, income tax, and property tax are all calculated as percentages of the taxable amount. Accurately calculating taxes necessitates proficiency in percentage calculations.
4. Statistics and Data Analysis:
Percentages are widely used to represent proportions in data analysis. For example, understanding the percentage of respondents who answered "yes" to a survey question is essential for interpreting the results. Percentage changes in data over time are also crucial for spotting trends and making informed decisions.
5. Everyday Life:
Calculating tips in restaurants, determining the percentage of completion of a project, or understanding nutritional information on food labels all involve percentage calculations.
Expanding Your Understanding: More Complex Percentage Problems
While "What percent of 5 is 2?" is a relatively straightforward problem, the principles involved can be applied to more complex scenarios. Let's explore some examples:
Example 1: Finding the Whole
If 30% of a number is 12, what is the number?
To solve this, we can set up a proportion:
30/100 = 12/x
Cross-multiplying and solving for x gives us:
30x = 1200
x = 40
Therefore, the number is 40.
Example 2: Finding the Part
What is 15% of 80?
Using the formula:
Percentage = (Part / Whole) * 100
We can rearrange it to find the part:
Part = (Percentage/100) * Whole
Substituting the values:
Part = (15/100) * 80 = 12
Therefore, 15% of 80 is 12.
Example 3: Percentage Increase/Decrease
A product's price increased from $20 to $25. What is the percentage increase?
First, find the difference: $25 - $20 = $5
Then, divide the difference by the original price and multiply by 100:
Percentage Increase = (5/20) * 100 = 25%
The price increased by 25%.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more confident and proficient you'll become.
- Use Different Methods: Try solving problems using proportions, formulas, and decimals to find the method you're most comfortable with.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Break Down Complex Problems: Divide complex problems into smaller, more manageable steps.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can help you improve your understanding of percentages.
Conclusion: The Power of Percentages
The seemingly simple question, "What percent of 5 is 2?" opens a door to a world of practical mathematical applications. Understanding percentage calculations is not just about solving mathematical problems; it's about developing a crucial skill that enhances your ability to analyze data, make informed decisions, and navigate the numerical world around you. By mastering these concepts, you equip yourself with a valuable tool for success in various aspects of life, from personal finance to professional endeavors. So, embrace the power of percentages and watch your understanding grow!
Latest Posts
Latest Posts
-
Least Common Multiple Of 6 And 30
May 23, 2025
-
How Many Years Is 1992 To 2024
May 23, 2025
-
12 Am To 12 Am Is How Many Hours
May 23, 2025
-
What Is 1 2 5 As A Fraction
May 23, 2025
-
What Year Was I Born If Im 58
May 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.