What Percent Is 8 Out Of 40
listenit
Apr 03, 2025 · 5 min read
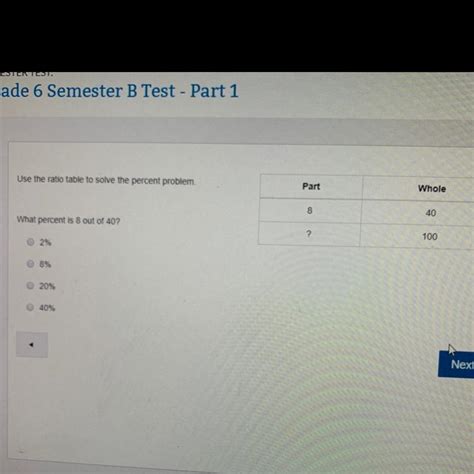
Table of Contents
What Percent is 8 out of 40? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the question, "What percent is 8 out of 40?", exploring various methods to solve this problem and expanding on the broader concept of percentage calculations. We'll cover not just the answer but also the underlying principles, practical applications, and advanced techniques to enhance your understanding.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. The word "percent" literally means "out of 100." Therefore, 50% means 50 out of 100, which can be simplified to ½ or 0.5. This concept is crucial for converting fractions and decimals into percentages and vice-versa.
Key Terms:
- Numerator: The top number in a fraction (in this case, 8).
- Denominator: The bottom number in a fraction (in this case, 40).
- Percentage: A fraction expressed as a number out of 100.
Calculating "What percent is 8 out of 40?"
There are several ways to solve this problem, each offering a slightly different approach and enhancing your understanding of percentage calculations:
Method 1: Using the Fraction Method
This is perhaps the most straightforward method. We begin by expressing the given numbers as a fraction:
8/40
Next, we simplify the fraction by finding the greatest common divisor (GCD) of both the numerator and the denominator. In this case, the GCD of 8 and 40 is 8. Dividing both the numerator and denominator by 8, we get:
1/5
Now, we need to convert this fraction to a percentage. To do this, we perform the following calculation:
(1/5) * 100% = 20%
Therefore, 8 out of 40 is 20%.
Method 2: Using the Decimal Method
This method involves converting the fraction directly to a decimal and then to a percentage.
-
Convert the fraction to a decimal: Divide the numerator (8) by the denominator (40): 8 ÷ 40 = 0.2
-
Convert the decimal to a percentage: Multiply the decimal by 100%: 0.2 * 100% = 20%
Again, we arrive at the answer: 8 out of 40 is 20%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion where 'x' represents the unknown percentage:
8/40 = x/100
To solve for 'x', we cross-multiply:
40x = 800
Now, divide both sides by 40:
x = 20
Therefore, x = 20%, confirming that 8 out of 40 is 20%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in various real-world scenarios. Here are a few examples:
1. Discounts and Sales
Retailers frequently advertise discounts as percentages. For example, a "20% off" sale means you pay 80% of the original price. Knowing how to calculate percentages allows you to quickly determine the final price after a discount.
2. Taxes and Interest
Taxes are often expressed as percentages of income or the value of goods and services. Similarly, interest rates on loans and investments are usually expressed as percentages. Understanding percentages helps you calculate the total amount you'll pay including taxes or the total return on your investment.
3. Data Analysis and Statistics
Percentages are widely used in data analysis and statistics to represent proportions and trends. For instance, you might see statistics presented as percentages showing the proportion of people who prefer a certain product or the percentage change in a company's profits over time.
4. Grade Calculations
In many educational systems, grades are expressed as percentages. Understanding percentages helps students understand their performance in a course and track their progress throughout the semester.
Beyond the Basics: Advanced Percentage Calculations
While the problem "What percent is 8 out of 40?" is relatively straightforward, understanding percentage calculations extends to more complex scenarios:
1. Calculating Percentage Increase or Decrease
These calculations involve determining the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100%
For example, if a product's price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] * 100% = 20%
2. Calculating Percentage of a Number
This involves finding a specific percentage of a given number. The formula is:
(Percentage/100) * Number
For example, to find 25% of 80, we calculate:
(25/100) * 80 = 20
3. Working Backwards from a Percentage
Sometimes, you might know the percentage and the resulting value but need to find the original value. This requires reversing the percentage calculation.
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and understanding the underlying concepts. Here are some tips to enhance your skills:
- Practice Regularly: Solve various percentage problems to build confidence and fluency.
- Use Multiple Methods: Try different methods to solve the same problem to gain a deeper understanding.
- Visual Aids: Use diagrams or charts to visualize the problem and solution.
- Real-World Applications: Apply your knowledge to real-world scenarios to reinforce your learning.
- Utilize Online Resources: Many online calculators and tutorials can help you practice and learn more about percentage calculations.
Conclusion
Understanding "what percent is 8 out of 40?" is more than just solving a simple math problem; it's about grasping the fundamental principles of percentage calculations. These principles have wide-ranging applications in various aspects of daily life, from personal finance to data analysis. By mastering these concepts and practicing regularly, you equip yourself with a valuable skill that will serve you well in various academic, professional, and personal endeavors. Remember to use different methods to solve percentage problems, apply your knowledge to real-world situations, and consistently practice to build a strong foundation in this essential area of mathematics.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 42 And 24
Apr 04, 2025
-
Whats The Square Root Of 250
Apr 04, 2025
-
Where Is Most Freshwater On Earth Found
Apr 04, 2025
-
Mars Distance From Earth In Light Years
Apr 04, 2025
-
What Energy Transformation Takes Place During Photosynthesis
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 8 Out Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
