What Percent Is 7 Of 12
listenit
May 11, 2025 · 4 min read
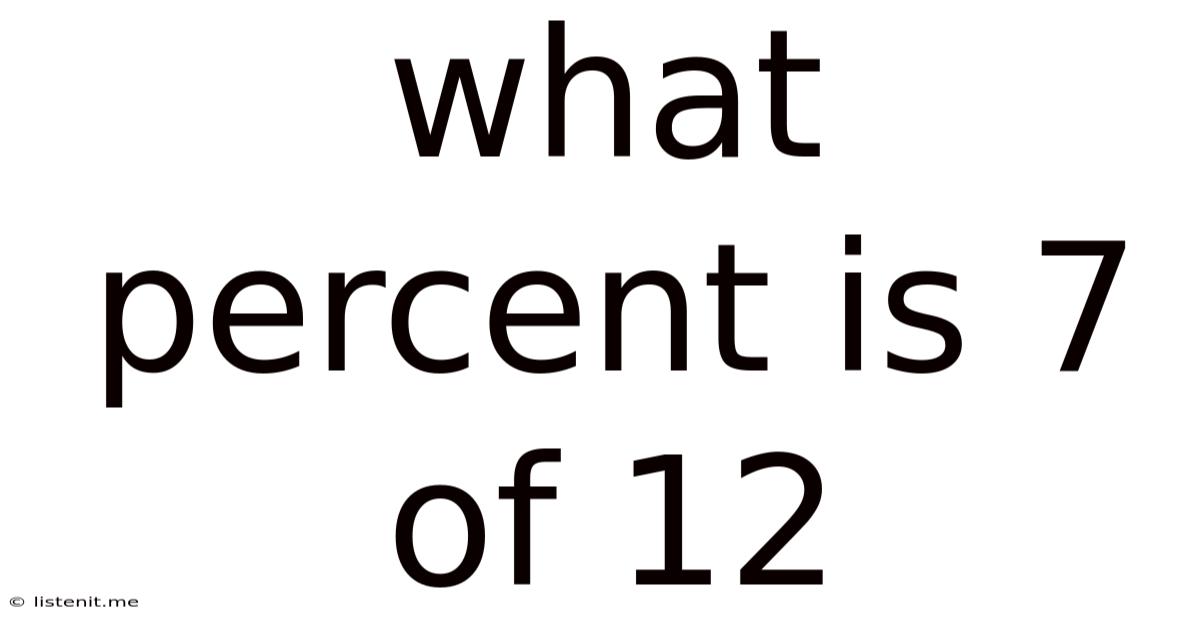
Table of Contents
What Percent is 7 of 12? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percent one number represents of another is crucial for interpreting data, making informed decisions, and generally navigating the quantitative aspects of life. This article will delve into the calculation of "What percent is 7 of 12?", exploring the methodology, providing multiple approaches, and expanding on the broader applications of percentage calculations.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" denotes this representation. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating "What Percent is 7 of 12?"
The core question is: what percentage does 7 represent when considering the whole as 12? We can solve this using several methods:
Method 1: The Fraction Method
The most intuitive method involves expressing the relationship between 7 and 12 as a fraction: 7/12. To convert this fraction into a percentage, we need to find an equivalent fraction with a denominator of 100. We achieve this by multiplying both the numerator and the denominator by a number that transforms the denominator into 100.
However, there isn't a whole number that directly converts 12 into 100. Therefore, we'll perform the division first:
7 ÷ 12 ≈ 0.5833
To convert this decimal to a percentage, we multiply by 100:
0.5833 × 100 ≈ 58.33%
Therefore, 7 is approximately 58.33% of 12.
Method 2: The Proportion Method
This method leverages the concept of proportions. We can set up a proportion where 'x' represents the unknown percentage:
7/12 = x/100
To solve for 'x', we cross-multiply:
12x = 700
x = 700/12
x ≈ 58.33
Thus, 7 is approximately 58.33% of 12.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 7 by 12 and then multiply the result by 100 to obtain the percentage.
7 ÷ 12 × 100 ≈ 58.33%
Rounding and Precision
The result of 58.33% is an approximation. The actual decimal value is a repeating decimal (0.583333...). The level of precision required depends on the context. In many cases, rounding to two decimal places (58.33%) is sufficient. However, for applications requiring higher accuracy, you might use more decimal places or express the answer as a fraction.
Practical Applications of Percentage Calculations
The ability to calculate percentages is indispensable in numerous real-world scenarios:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest relies heavily on percentage calculations.
- Discounts and Sales Tax: Determining the final price of an item after a discount or adding sales tax involves percentage computations.
- Investment Returns: Tracking investment performance and calculating returns on investment require understanding percentage change.
- Budgeting: Allocating funds across different categories of a budget often involves expressing each category as a percentage of the total budget.
2. Data Analysis and Interpretation:
- Statistical Analysis: Percentages are crucial for expressing proportions, frequencies, and probabilities in statistical analysis.
- Market Research: Analyzing survey data and market trends frequently involves representing findings as percentages.
- Scientific Research: Percentages are used to express changes in experimental measurements, proportions in populations, and various other quantitative aspects.
3. Everyday Life:
- Shopping: Comparing prices and evaluating deals often requires calculating percentage discounts.
- Tipping: Determining the appropriate tip amount in restaurants involves calculating a percentage of the bill.
- Grading: Many grading systems use percentages to represent a student's performance on assessments.
- Cooking: Scaling recipes up or down often requires adjusting ingredient quantities by percentages.
Expanding on Percentage Concepts
Beyond the basic calculation, understanding related concepts strengthens your overall understanding of percentages:
Percentage Change:
This represents the relative change between two values. It's calculated as: [(New Value - Old Value) / Old Value] x 100%. A positive result signifies an increase, while a negative result signifies a decrease.
Percentage Points:
This refers to the absolute difference between two percentages. For example, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, not 60% (which would be the percentage change).
Conclusion
Calculating "what percent is 7 of 12" is a straightforward yet fundamental percentage problem. Mastering this calculation, along with understanding related percentage concepts and their applications, is vital for navigating the quantitative aspects of various domains, from personal finance to professional endeavors. The multiple methods presented – the fraction method, the proportion method, and using a calculator – offer flexibility depending on the situation and individual preference. Remember that the precision of your answer should align with the context of the problem. By building a strong foundation in percentage calculations, you equip yourself with a valuable tool for informed decision-making and a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
What Is The Distance Between 4 7 And 2 2
May 13, 2025
-
Fes Spell Out The Full Name Of The Compound
May 13, 2025
-
How Many Equilateral Triangles Are There In A Regular Hexagon
May 13, 2025
-
What Is The Main Goal Of Photosynthesis
May 13, 2025
-
What Is The Number Of Neutrons In Fluorine
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 7 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.