What Percent Is 1 Out Of 11
listenit
May 24, 2025 · 4 min read
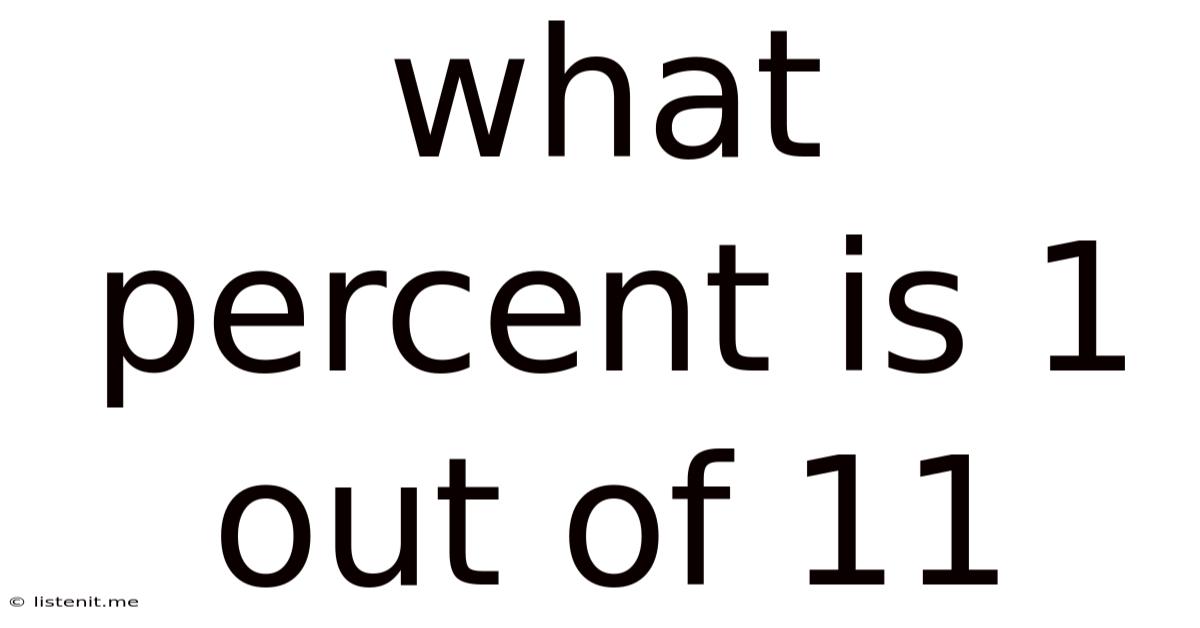
Table of Contents
What Percent is 1 out of 11? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex statistical analysis and scientific research. This article delves into the question, "What percent is 1 out of 11?", providing not only the answer but also a comprehensive understanding of the underlying principles and various methods for solving similar percentage problems. We'll explore different calculation approaches, discuss their applications, and offer practical examples to solidify your grasp of this essential mathematical concept.
Understanding the Basics of Percentages
A percentage is simply a fraction expressed as a portion of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Calculating "What Percent is 1 out of 11?"
The core of the problem lies in converting the fraction 1/11 into a percentage. We can achieve this using several methods:
Method 1: Direct Conversion using Division
The simplest method involves dividing the numerator (1) by the denominator (11) and then multiplying the result by 100 to express the answer as a percentage.
1 ÷ 11 ≈ 0.0909
0.0909 x 100 ≈ 9.09%
Therefore, 1 out of 11 is approximately 9.09%.
Method 2: Fraction to Decimal to Percentage
This method breaks down the process into two steps:
-
Fraction to Decimal: Convert the fraction 1/11 into a decimal by performing the division: 1 ÷ 11 ≈ 0.0909
-
Decimal to Percentage: Multiply the decimal by 100 to express it as a percentage: 0.0909 x 100 ≈ 9.09%
Again, we arrive at the same answer: approximately 9.09%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion:
1/11 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
11x = 100
x = 100/11 ≈ 9.09
Therefore, 1 out of 11 is approximately 9.09%.
Understanding the Significance of Rounding
Notice that in all the methods, we obtained an approximate value of 9.09%. This is because the decimal representation of 1/11 is a recurring decimal (0.090909...). Depending on the context, you might need to round the result to a specific number of decimal places. For many practical purposes, rounding to two decimal places (9.09%) is sufficient. However, in situations requiring higher precision, you may need to use more decimal places or express the answer as a fraction.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Retail: Determining sale prices, calculating markups, and analyzing sales data.
-
Science: Representing experimental results, expressing statistical probabilities, and calculating error margins.
-
Everyday Life: Tip calculations in restaurants, understanding sale discounts, and determining the percentage of a task completed.
Advanced Percentage Calculations and Related Concepts
Beyond the basic calculation of "what percent is 1 out of 11?", understanding percentages extends to more complex scenarios:
-
Percentage Change: This involves calculating the percentage increase or decrease between two values. The formula is: [(New Value - Old Value) / Old Value] x 100.
-
Percentage Points: This represents the arithmetic difference between two percentages, not the percentage change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a critical concept in finance and investment.
-
Statistical Analysis: Percentages are used extensively in statistical analysis to represent proportions, probabilities, and confidence intervals.
Troubleshooting Common Percentage Calculation Errors
Common mistakes in percentage calculations include:
-
Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
-
Rounding Errors: Be mindful of rounding errors, especially when performing multiple calculations. Round only at the final step to minimize inaccuracies.
-
Confusing Percentage Change and Percentage Points: Clearly differentiate between percentage change and percentage points to avoid misinterpretations.
Expanding Your Understanding of Percentages
To further enhance your understanding and proficiency in percentage calculations, consider:
-
Practicing Regularly: Work through various examples and practice problems to build your confidence and skill.
-
Using Online Calculators: Utilize online percentage calculators to verify your answers and explore different approaches. (Note: While helpful for checking your work, rely on understanding the underlying principles rather than solely depending on calculators.)
-
Exploring Advanced Topics: Delve into more advanced percentage-related concepts like compound interest and statistical analysis to expand your mathematical knowledge.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, particularly problems like "what percent is 1 out of 11?", is a fundamental skill with broad applications. By grasping the different calculation methods, understanding the significance of rounding, and being aware of potential errors, you can confidently tackle various percentage-related challenges in your academic, professional, and personal life. Remember that consistent practice and exploration of related concepts are key to mastering this essential mathematical skill. The ability to quickly and accurately calculate percentages not only demonstrates numerical literacy but also enhances problem-solving capabilities across diverse fields.
Latest Posts
Latest Posts
-
What Is 75 Off Of 25
May 24, 2025
-
What Is The Least Common Multiple Of 10 And 20
May 24, 2025
-
What Is 11111 As A Fraction
May 24, 2025
-
25 Meters Per Second To Mph
May 24, 2025
-
What Is 2 2 In A Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 1 Out Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.