What Is The Square Root Of 53
listenit
Apr 07, 2025 · 5 min read
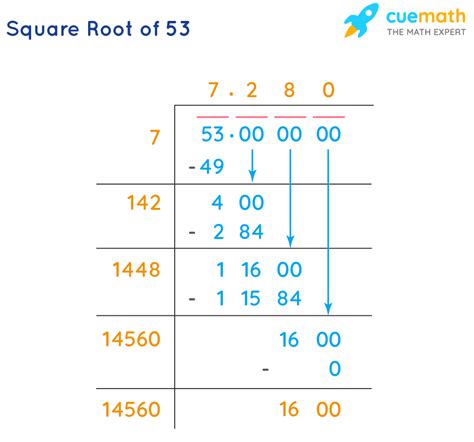
Table of Contents
What is the Square Root of 53? A Deep Dive into Irrational Numbers
The question, "What is the square root of 53?" seems simple enough. However, exploring this seemingly straightforward mathematical concept opens a door to a fascinating world of irrational numbers, approximation techniques, and the beauty of mathematical precision. This article will delve into the square root of 53, exploring its properties, how to calculate it, and its significance within the broader landscape of mathematics.
Understanding Square Roots
Before we tackle the square root of 53 specifically, let's establish a foundational understanding of square roots. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This is denoted as √9 = 3.
However, not all numbers have whole number square roots. Many numbers, including 53, have square roots that are irrational numbers. This means their decimal representation goes on forever without repeating. This is a key characteristic that differentiates them from rational numbers (which can be expressed as a fraction of two integers).
Calculating the Square Root of 53
There's no simple, exact way to express the square root of 53 as a fraction or a terminating decimal. However, we can employ several methods to approximate its value:
1. Using a Calculator
The easiest way to find an approximation is using a calculator. Most calculators will provide a decimal approximation of √53 to several decimal places. You'll typically find a value around 7.280109889…. Note the ellipsis (...) indicating that the decimal continues infinitely.
2. The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation of a square root. It works by repeatedly refining an initial guess. Let's outline the steps:
-
Make an initial guess: Let's start with a guess of 7 (since 7 x 7 = 49, which is close to 53).
-
Refine the guess: Divide the number (53) by the guess (7): 53 / 7 ≈ 7.57.
-
Average the guess and the result: Average the initial guess (7) and the result from step 2 (7.57): (7 + 7.57) / 2 ≈ 7.285.
-
Repeat: Use the new average (7.285) as the new guess and repeat steps 2 and 3. The more iterations you perform, the closer your approximation will get to the true value.
By repeating this process several times, you'll converge on a value increasingly close to the actual square root of 53.
3. Using the Binomial Theorem
The binomial theorem allows us to approximate square roots by expanding a binomial expression. While computationally more complex than the Babylonian method, it provides a powerful tool for precise approximations. The approach involves expressing the square root as a binomial series and calculating terms up to a desired level of accuracy. This method is often used in advanced mathematical contexts and requires a solid understanding of calculus.
The Significance of Irrational Numbers
The fact that √53 is irrational highlights the richness and complexity of the number system. While we can only approximate its value, its existence as an irrational number is fundamental to mathematical understanding. Irrational numbers are essential in various areas of mathematics, including:
-
Geometry: Irrational numbers frequently arise in geometric calculations, such as finding the diagonal of a square or the circumference of a circle. The famous irrational number π (pi) is a prime example, representing the ratio of a circle's circumference to its diameter.
-
Calculus: Irrational numbers are fundamental to calculus and the study of continuous functions and limits. Many important mathematical constants, like e (Euler's number), are irrational.
-
Trigonometry: Trigonometric functions often involve irrational numbers, such as the values of sine, cosine, and tangent for certain angles.
-
Algebra: Solving quadratic equations sometimes yields irrational roots, demonstrating the interconnectedness of different mathematical fields.
Practical Applications of Square Roots
While the square root of 53 might not seem directly applicable to everyday life, the concept of square roots finds extensive use in various fields:
-
Physics: Calculating velocity, acceleration, and other physical quantities frequently involves the use of square roots. For example, calculating the distance an object has traveled given its acceleration and time.
-
Engineering: Square roots are essential in structural engineering calculations, such as determining the stress on a material or the stability of a structure.
-
Finance: Calculating compound interest involves the use of square roots, as does the determination of the time it takes to double an investment.
-
Computer Graphics: Square roots are used extensively in computer graphics and game development for calculating distances and positions in 2D and 3D space.
Approximating √53: A Deeper Look at the Babylonian Method
Let's illustrate the Babylonian method with a few more iterations to demonstrate its convergence toward the actual value:
Iteration 1:
- Initial guess: 7
- 53 / 7 ≈ 7.5714
- Average: (7 + 7.5714) / 2 ≈ 7.2857
Iteration 2:
- New guess: 7.2857
- 53 / 7.2857 ≈ 7.2801
- Average: (7.2857 + 7.2801) / 2 ≈ 7.2829
Iteration 3:
- New guess: 7.2829
- 53 / 7.2829 ≈ 7.2801
- Average: (7.2829 + 7.2801) / 2 ≈ 7.2815
As you can see, with each iteration, the approximation gets progressively closer to the actual value of √53 (approximately 7.280109889...). The speed of convergence depends on the initial guess and the precision required.
Conclusion: Embracing the Irrational
The square root of 53, though irrational, is a fascinating mathematical entity. While we can't express it as a simple fraction or a terminating decimal, understanding its properties and the methods used to approximate its value allows us to appreciate the elegance and power of mathematics. Its presence underscores the importance of irrational numbers in various fields, from abstract mathematical theories to practical applications in science and engineering. The pursuit of understanding √53—and irrational numbers in general—demonstrates the ongoing exploration and precision that define the mathematical world. And that, in itself, is a beautiful thing.
Latest Posts
Latest Posts
-
3 Is 40 Percent Of What
Apr 08, 2025
-
How Many Units In A Milligram
Apr 08, 2025
-
Graph Of Absolute Value Of X 1
Apr 08, 2025
-
What Are The Steps Of The Dna Ladder Made Of
Apr 08, 2025
-
The True Power Is Dissipated By The Of Any Circuit
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 53 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.