What Is The Square Root Of 2.25
listenit
Apr 05, 2025 · 5 min read
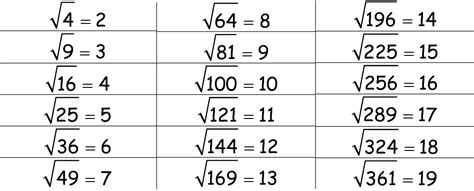
Table of Contents
What is the Square Root of 2.25? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 2.25?" opens a door to a fascinating world of mathematics, encompassing concepts from basic arithmetic to advanced algebraic techniques. This article will not only answer that question definitively but also explore the broader context of square roots, their properties, and their widespread applications across various fields.
Understanding Square Roots: A Foundational Concept
Before diving into the specifics of the square root of 2.25, let's establish a solid understanding of what a square root actually is. In essence, the square root of a number is a value that, when multiplied by itself (squared), results in the original number. For instance, the square root of 9 is 3 because 3 x 3 = 9. This can be expressed mathematically as:
√9 = 3
The symbol '√' denotes the square root operation. It's important to note that most positive numbers have two square roots: a positive and a negative one. For example, both 3 and -3, when squared, yield 9. However, unless otherwise specified, the principal square root (the positive one) is typically considered.
Calculating the Square Root of 2.25: Methods and Approaches
There are several ways to calculate the square root of 2.25. Let's explore a few:
1. The Direct Method (for Perfect Squares):
The most straightforward approach is to recognize that 2.25 is a perfect square. This means it's the result of squaring a rational number. Through trial and error, or by recalling common squares, we find that:
1.5 x 1.5 = 2.25
Therefore:
√2.25 = 1.5
This method works best when dealing with perfect squares, numbers that are the product of an integer multiplied by itself.
2. Prime Factorization Method:
This method is particularly useful for larger numbers. While 2.25 isn't a whole number, we can work with its fractional equivalent, 9/4. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves).
- Convert to a fraction: 2.25 = 9/4
- Factor the numerator and denominator: 9 = 3 x 3 and 4 = 2 x 2
- Rewrite the fraction using prime factors: (3 x 3) / (2 x 2)
- Apply the square root: √[(3 x 3) / (2 x 2)] = √(3²) / √(2²) = 3/2 = 1.5
This method highlights the properties of square roots with fractions.
3. Using a Calculator:
For more complex numbers, a calculator is the most efficient tool. Simply input 2.25 and press the square root button (√) to obtain the answer: 1.5.
4. The Babylonian Method (Iterative Approach):
For numbers that aren't perfect squares, iterative methods like the Babylonian method (also known as Heron's method) provide an approximation. This method involves refining an initial guess through repeated calculations. While not strictly necessary for 2.25 (since it's a perfect square), it's a valuable technique for understanding how square root calculations are approximated for non-perfect squares.
The Babylonian method involves the following iterative formula:
x_(n+1) = 0.5 * (x_n + S/x_n)
Where:
- x_n is the current guess
- x_(n+1) is the improved guess
- S is the number whose square root is being calculated
Let's demonstrate this with an initial guess of 1.4 for √2.25:
- Iteration 1: x_1 = 0.5 * (1.4 + 2.25/1.4) ≈ 1.507
- Iteration 2: x_2 = 0.5 * (1.507 + 2.25/1.507) ≈ 1.50002
- Iteration 3: x_3 = 0.5 * (1.50002 + 2.25/1.50002) ≈ 1.5
As you can see, the method rapidly converges to the correct answer.
Applications of Square Roots in Real-World Scenarios
The concept of square roots extends far beyond simple mathematical exercises. They are fundamental to numerous fields, including:
1. Geometry and Trigonometry:
Square roots are essential in calculating distances, areas, and volumes. The Pythagorean theorem, a cornerstone of geometry, uses square roots to determine the length of the hypotenuse of a right-angled triangle:
c = √(a² + b²)
where 'a' and 'b' are the lengths of the other two sides, and 'c' is the hypotenuse. Trigonometry also relies heavily on square roots, particularly in calculations involving angles and distances.
2. Physics and Engineering:
Square roots appear frequently in physics equations. For example, calculating the velocity of an object using kinetic energy involves a square root:
v = √(2KE/m)
where 'KE' is kinetic energy and 'm' is mass. Engineering applications, such as structural design and calculating forces, also utilize square roots extensively.
3. Finance and Economics:
In finance, standard deviation, a measure of risk and volatility, involves calculating the square root of variance. This helps investors assess the risk associated with different investments.
4. Computer Graphics and Game Development:
Square roots are crucial in computer graphics and game development for calculations involving distances, rotations, and transformations of objects in three-dimensional space.
5. Statistics and Data Analysis:
Standard error, used in hypothesis testing and confidence intervals, involves calculating the square root of the variance. This measure quantifies the uncertainty in an estimate.
Beyond the Square Root of 2.25: Exploring Higher-Order Roots
While this article has focused primarily on square roots, it's worth briefly mentioning higher-order roots. These include cube roots (∛), fourth roots (∜), and so on. These roots represent values that, when multiplied by themselves a specific number of times, yield the original number. For instance, the cube root of 8 is 2 because 2 x 2 x 2 = 8.
The concepts and techniques discussed regarding square roots can be extended to these higher-order roots as well, highlighting the interconnectedness and fundamental nature of these mathematical concepts.
Conclusion: The Significance of Understanding Square Roots
The square root of 2.25, while a seemingly simple calculation, serves as an excellent entry point for understanding the broader significance of square roots in mathematics and its applications. From geometry and trigonometry to physics, finance, and computer science, square roots are integral to numerous fields, enabling the solution of complex problems and the modeling of real-world phenomena. Mastering the concept of square roots is a foundational step towards a deeper understanding of mathematics and its pervasive influence on various aspects of our lives. Whether you are a student, a professional, or simply someone curious about the world of numbers, understanding square roots and their applications is an enriching and valuable endeavor.
Latest Posts
Latest Posts
-
12 Is 60 Percent Of What Number
Apr 06, 2025
-
Find Radian Measure Of Central Angle
Apr 06, 2025
-
How Many Molecules In An Atom
Apr 06, 2025
-
Is H2o An Acid Or Base
Apr 06, 2025
-
Explain How Fluctuations In Abiotic Cycles Can Influence Populations
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 2.25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
