What Is The Square Root Of 192
listenit
Mar 26, 2025 · 4 min read
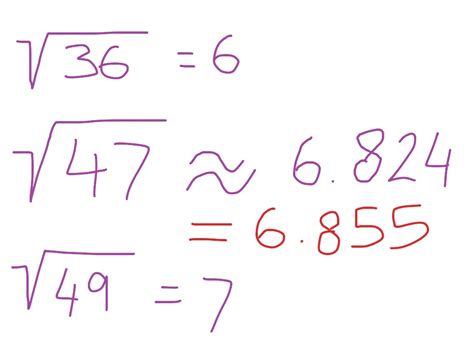
Table of Contents
What is the Square Root of 192? A Deep Dive into Simplification and Approximation
The question, "What is the square root of 192?" might seem simple at first glance. However, exploring this seemingly straightforward mathematical problem opens doors to a deeper understanding of square roots, prime factorization, and various approximation techniques. This article will not only answer the question but also delve into the methods used to arrive at the solution, providing a comprehensive guide for both beginners and those seeking a more thorough understanding.
Understanding Square Roots
Before tackling the square root of 192, let's solidify our understanding of what a square root represents. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This is often represented mathematically as √9 = 3. However, not all square roots result in whole numbers. Many produce irrational numbers—numbers that cannot be expressed as a simple fraction and have an infinite number of decimal places.
Finding the Square Root of 192: The Prime Factorization Method
The most common and accurate method for simplifying a square root like √192 involves prime factorization. This technique breaks down the number into its prime components—numbers divisible only by 1 and themselves. Let's break down 192 into its prime factors:
- Divide by 2: 192 ÷ 2 = 96
- Divide by 2 again: 96 ÷ 2 = 48
- Divide by 2 again: 48 ÷ 2 = 24
- Divide by 2 again: 24 ÷ 2 = 12
- Divide by 2 again: 12 ÷ 2 = 6
- Divide by 2 again: 6 ÷ 2 = 3
Therefore, the prime factorization of 192 is 2 x 2 x 2 x 2 x 2 x 2 x 3, or 2⁶ x 3.
Now, we can rewrite the square root of 192 using this factorization:
√192 = √(2⁶ x 3)
Since √(a x b) = √a x √b, we can simplify further:
√192 = √(2⁶) x √3
Because √(2⁶) is the same as √(2² x 2² x 2²), this simplifies to 2 x 2 x 2 x √3 = 8√3.
Therefore, the simplified square root of 192 is 8√3. This is the exact answer, and it's often preferred in mathematical contexts because it retains precision.
Approximating the Square Root of 192
While 8√3 is the exact value, it's sometimes useful to have a decimal approximation. To achieve this, we can use a calculator or an approximation method.
Using a calculator, we find that:
√192 ≈ 13.8564 (rounded to five decimal places)
Alternative Approximation Techniques
While a calculator provides the quickest approximation, understanding alternative methods is valuable for building a deeper understanding of square roots. Here are a couple of methods:
1. Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively get closer to the actual square root. Let's start with an initial guess of 14:
- Divide the number by the guess: 192 ÷ 14 ≈ 13.714
- Average the guess and the result: (14 + 13.714) ÷ 2 ≈ 13.857
- Repeat steps 1 and 2 using the new average as the guess: This process can be repeated until the desired level of accuracy is achieved. Each iteration brings the approximation closer to the actual value.
2. Linear Approximation
This method uses the tangent line of the square root function at a known point to estimate the square root of a nearby number. While less precise than the Babylonian method, it provides a quicker, albeit rougher, estimate.
Practical Applications of Square Roots
Understanding square roots isn't just an academic exercise; it has numerous practical applications across various fields:
- Geometry: Calculating the diagonal of a square or rectangle involves the Pythagorean theorem, which utilizes square roots.
- Physics: Many physics equations, especially those involving motion and energy, use square roots.
- Engineering: Structural engineers use square roots in calculations related to stress, strain, and stability.
- Computer Graphics: Square roots are integral to various calculations in 3D rendering and animation.
- Statistics: Standard deviation, a crucial concept in statistics, involves calculating square roots.
Beyond the Basics: Exploring Higher-Order Roots
While we've focused on square roots (the second root), it's important to know that higher-order roots exist. A cube root (third root) is a number that, when multiplied by itself three times, equals the original number (e.g., ³√8 = 2 because 2 x 2 x 2 = 8). Similarly, fourth roots, fifth roots, and so on, can be calculated. These higher-order roots share similar properties and solution methods to square roots, utilizing factorization and approximation techniques.
Conclusion: Mastering the Square Root of 192 and Beyond
The seemingly simple question, "What is the square root of 192?" has led us on a journey through prime factorization, approximation techniques, and practical applications. Understanding the fundamental concepts of square roots is crucial for various mathematical and scientific endeavors. Whether you prefer the exact simplified form (8√3) or a decimal approximation (13.8564), the process of arriving at the answer has provided valuable insights into a key mathematical concept. Remember that mastering this concept builds a strong foundation for more complex mathematical explorations. By understanding the underlying principles, you’re not just calculating a number; you're building a deeper appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Inverse Function Of X 3 X 2
Mar 29, 2025
-
Why Are Most Fossils Found In Sedimentary Rocks
Mar 29, 2025
-
What Is The Gcf Of 45 And 36
Mar 29, 2025
-
What Number Is 45 Of 90
Mar 29, 2025
-
What Is 2 5 As A Decimal
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 192 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
