What Is The Radian Of 45 Degrees
listenit
Apr 01, 2025 · 5 min read
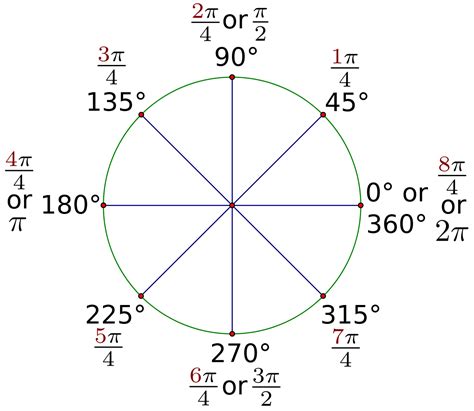
Table of Contents
What is the Radian of 45 Degrees? A Comprehensive Guide
Radians and degrees are both units used to measure angles, much like centimeters and inches are both used to measure length. While degrees are more familiar in everyday life, radians are fundamental in many areas of mathematics, particularly calculus and higher-level trigonometry. Understanding the relationship between radians and degrees is crucial for anyone working with angles in a mathematical context. This article will delve deep into understanding what a radian is, how it relates to 45 degrees, and its significance in various mathematical applications.
Understanding Radians
A radian is defined as the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. Imagine a circle with a radius r. If you take a piece of string equal to the length of the radius and place it along the circumference of the circle, the angle formed at the center by that arc is one radian.
This definition is crucial because it connects the measurement of an angle directly to the geometry of the circle. It's a geometric definition, not an arbitrary one like the degree system. The degree system, which divides a full circle into 360 degrees, is a historical convention that doesn't have this inherent geometric relationship.
Visualizing a Radian
It's helpful to visualize a radian. Picture a circle. Now, imagine placing the radius along the circumference. The angle formed at the center is one radian. You can't easily divide a circle into neat sections using radians like you can with degrees (360, 180, 90, etc.). This is because the radian is a measure based on the relationship between the radius and the circumference.
Why Use Radians?
While degrees are intuitive for everyday use, radians offer significant advantages, particularly in calculus and advanced mathematics:
-
Simplicity in Calculus: Many formulas in calculus involving angles, such as derivatives and integrals of trigonometric functions, are significantly simpler and more elegant when using radians. Using degrees would require cumbersome conversion factors.
-
Natural Unit: Radians are a natural unit of angular measurement because they are directly related to the circle's radius and circumference. This makes them inherently more suitable for geometric and physical applications where the circle's geometry is central.
-
Relationship to Arc Length: The arc length (s) of a circle segment is directly related to the angle (θ) in radians and the radius (r) by the simple formula:
s = rθ. This formula doesn't work with degrees without a conversion factor. -
Unitless Nature (in many contexts): While radians technically have units, in many formulas they effectively act as dimensionless quantities, simplifying calculations.
Converting Degrees to Radians
The fundamental relationship between radians and degrees comes from the fact that there are 2π radians in a full circle (360 degrees). This allows us to develop a conversion factor:
180 degrees = π radians
This equation is the cornerstone of all degree-to-radian conversions. To convert degrees to radians, we use the following formula:
Radians = (Degrees * π) / 180
Calculating the Radian of 45 Degrees
Now, let's apply this knowledge to find the radian equivalent of 45 degrees. Using the formula above:
Radians = (45° * π) / 180°
Simplifying this expression:
Radians = π / 4
Therefore, 45 degrees is equal to π/4 radians. This is a commonly used angle in trigonometry and other mathematical fields.
Significance of π/4 Radians (45 Degrees)
The angle of π/4 radians (45 degrees) holds particular significance in trigonometry and geometry:
-
Isosceles Right-Angled Triangle: A 45-degree angle forms one of the acute angles in an isosceles right-angled triangle. This triangle is fundamental in various geometric problems.
-
Trigonometric Values: The trigonometric functions (sine, cosine, and tangent) have easily calculable values for 45 degrees (or π/4 radians):
- sin(π/4) = cos(π/4) = √2/2 ≈ 0.707
- tan(π/4) = 1
These simple values make π/4 radians a convenient angle for calculations.
-
Unit Circle: On the unit circle (a circle with radius 1), the coordinates of the point corresponding to an angle of π/4 radians are (√2/2, √2/2). This is a significant point on the unit circle used extensively in trigonometry.
-
Applications in Physics and Engineering: The angle of 45 degrees (π/4 radians) frequently appears in physics and engineering problems involving projectile motion, vectors, and wave phenomena. For example, to achieve the maximum range of a projectile, ignoring air resistance, the launch angle should be 45 degrees.
Radians in Advanced Mathematical Contexts
The use of radians becomes even more critical in advanced mathematical contexts:
-
Calculus: As mentioned earlier, using radians simplifies derivatives and integrals of trigonometric functions significantly. Formulas like the derivative of sin(x) are only valid when x is measured in radians.
-
Complex Analysis: Radians are essential in complex analysis, a branch of mathematics dealing with complex numbers. Euler's formula, e^(ix) = cos(x) + i sin(x), is only valid when x is in radians. This formula connects exponential functions with trigonometric functions in a remarkably elegant way.
-
Differential Equations: Many differential equations involving oscillations and waves are more easily solved when angles are expressed in radians.
-
Fourier Analysis: Fourier analysis, a powerful technique for decomposing functions into simpler periodic components, relies heavily on the use of radians.
Conclusion: The Importance of Understanding Radians
While degrees are familiar for everyday angle measurements, radians are the preferred unit in almost all areas of advanced mathematics, physics, and engineering. Understanding the definition of a radian, its relationship to degrees, and its significance in various mathematical formulas and applications is crucial for anyone pursuing studies in these fields. The seemingly simple conversion of 45 degrees to π/4 radians unlocks a world of elegant mathematical relationships and simplifies complex calculations. Mastering the use of radians will significantly enhance your mathematical skills and understanding of the world around us. This simple yet powerful concept forms the foundation for numerous advanced mathematical concepts. Further exploration of this topic will undoubtedly lead to a more profound understanding of the interconnectedness of mathematics and its applications.
Latest Posts
Latest Posts
-
Finding The Angle Between Two Planes
Apr 02, 2025
-
What Are The Common Multiples Of 2 And 7
Apr 02, 2025
-
Ratio Of Each 90 If Ratio Is 7 3
Apr 02, 2025
-
Density Of Water At 4 C
Apr 02, 2025
-
Select The Graphs That Have An Equation With A 0
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Radian Of 45 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
