What Is The Prime Factor Of 135
listenit
May 26, 2025 · 5 min read
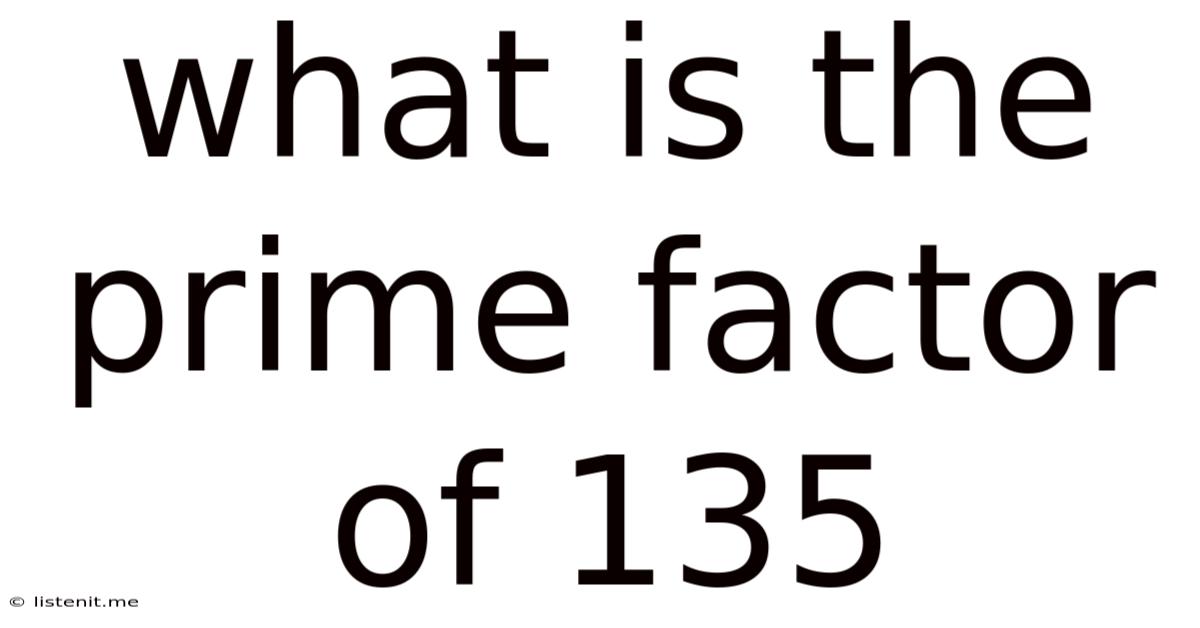
Table of Contents
What is the Prime Factor of 135? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple arithmetic exercise, but it's a fundamental concept in number theory with far-reaching applications in cryptography, computer science, and other fields. This article will delve into the prime factorization of 135, exploring the process, explaining the underlying concepts, and illustrating the broader significance of prime numbers and prime factorization.
Understanding Prime Numbers
Before we tackle the prime factorization of 135, let's establish a clear understanding of what a prime number is. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is neither prime nor composite.
Key characteristics of prime numbers:
- Divisibility: Only divisible by 1 and itself.
- Infinitude: There are infinitely many prime numbers. This was proven by Euclid centuries ago.
- Fundamental Theorem of Arithmetic: Every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors). This theorem forms the bedrock of prime factorization.
What is Prime Factorization?
Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. These factors are prime numbers that, when multiplied together, result in the original composite number. It's like finding the "building blocks" of a number, expressed solely in terms of prime numbers.
For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). This means that 2 and 3 are the prime factors of 12.
Finding the Prime Factors of 135: A Step-by-Step Approach
Now, let's find the prime factorization of 135. We'll use a method called the factor tree.
-
Start with the smallest prime number: We begin by dividing 135 by the smallest prime number, which is 2. Since 135 is an odd number, it's not divisible by 2.
-
Try the next prime number: The next prime number is 3. 135 divided by 3 is 45. So, we have: 135 = 3 x 45.
-
Continue factoring: Now, we need to factor 45. 45 is also divisible by 3, resulting in 15. So, we have: 135 = 3 x 3 x 15.
-
Factor further: 15 is divisible by 3, resulting in 5. Therefore, we have: 135 = 3 x 3 x 3 x 5.
-
Identify the prime factors: We've reached the point where all the factors are prime numbers (3 and 5). Therefore, the prime factorization of 135 is 3 x 3 x 3 x 5, or 3³ x 5.
Visual Representation (Factor Tree):
135
/ \
3 45
/ \
3 15
/ \
3 5
Significance of Prime Factorization
The seemingly simple act of finding prime factors has profound implications across various disciplines:
1. Cryptography:
Prime numbers are the cornerstone of modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring extremely large numbers into their prime factors. The larger the numbers, the more computationally expensive the factorization becomes, making it practically impossible to crack the encryption in a reasonable timeframe.
2. Computer Science:
Prime factorization plays a role in various computer science algorithms, including:
- Hashing: Prime numbers are often used in hash functions to minimize collisions and distribute data evenly.
- Random Number Generation: Prime numbers are crucial in generating pseudo-random numbers, vital for simulations, cryptography, and other applications.
3. Number Theory:
Prime factorization is fundamental to many theorems and concepts in number theory, providing insights into the structure and properties of integers. The distribution of prime numbers, the search for large primes, and the Riemann Hypothesis (a famous unsolved problem in mathematics related to prime numbers) are all active areas of research in number theory.
4. Other Applications:
Prime factorization finds applications in various other areas, including:
- Coding Theory: Error-correcting codes utilize prime numbers to improve efficiency and reliability.
- Chemistry: Prime numbers can sometimes be used in models and representations of chemical structures and reactions.
Beyond 135: Exploring Prime Factorization Techniques
While the factor tree method is effective for smaller numbers like 135, more sophisticated algorithms are needed for larger numbers. These algorithms include:
- Trial Division: Systematically dividing the number by successive prime numbers until all prime factors are found.
- Pollard's Rho Algorithm: A probabilistic algorithm used to find small prime factors efficiently.
- General Number Field Sieve (GNFS): The fastest known algorithm for factoring very large numbers, used in breaking RSA encryption (though still computationally expensive for extremely large numbers).
These algorithms highlight the computational complexity associated with prime factorization, which underlies the security of many cryptographic systems.
Conclusion: The Enduring Importance of Prime Numbers
The prime factorization of 135 (3³ x 5) might appear to be a simple mathematical calculation. However, understanding this process reveals the fundamental role prime numbers play in mathematics and its applications in various fields. From securing online transactions to advancing theoretical mathematics, the seemingly humble prime number remains an object of enduring fascination and importance in the world of numbers. The seemingly simple question – "What is the prime factor of 135?" – opens a door to a vast and fascinating world of mathematical exploration. This deep dive into prime factorization hopefully enhances your understanding and appreciation for these building blocks of numbers.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 3 And 6
May 26, 2025
-
72 Hours From Now Is What Day
May 26, 2025
-
Round 583027 74847 To The Nearest Hundred
May 26, 2025
-
How Many Calories Should A 145 Pound Woman Eat
May 26, 2025
-
How Many Calories To Maintain 130 Pounds Female
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factor Of 135 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.