What Is The Positive Square Root Of 36
listenit
Apr 08, 2025 · 6 min read
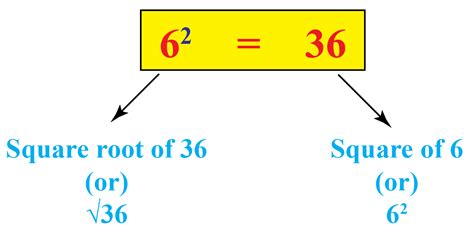
Table of Contents
What is the Positive Square Root of 36? A Deep Dive into Square Roots and Their Applications
The question, "What is the positive square root of 36?" seems deceptively simple. The answer, 6, is readily apparent to anyone familiar with basic arithmetic. However, delving deeper into this seemingly straightforward concept reveals a wealth of mathematical intricacies and practical applications across numerous fields. This article will explore the concept of square roots, focusing on the positive square root of 36, and examining its relevance in various contexts.
Understanding Square Roots
A square root is a number that, when multiplied by itself, equals a given number. In other words, if x² = y, then x is the square root of y. This concept is fundamental to algebra and numerous other branches of mathematics. We represent the square root using the radical symbol (√). Therefore, the square root of y is written as √y.
Every positive number has two square roots: one positive and one negative. For example, the square roots of 25 are +5 and -5, because both 5 × 5 = 25 and -5 × -5 = 25. However, when we talk about the square root of a number, we usually mean the principal square root, which is the non-negative square root.
The Positive Square Root of 36: A Simple Solution
Returning to our initial question, the positive square root of 36 is 6. This is because 6 multiplied by itself (6 × 6) equals 36. The negative square root of 36 is -6, since (-6) × (-6) also equals 36. But as we're focusing on the positive square root, our answer remains definitively 6.
Beyond the Basics: Exploring the Properties of Square Roots
Understanding the positive square root of 36 provides a solid foundation for exploring more complex properties of square roots:
1. Simplifying Square Roots:
Often, we encounter square roots that are not perfect squares (like √36). In such cases, we simplify the square root by factoring the number under the radical. For example, let's simplify √72:
- √72 = √(36 × 2) = √36 × √2 = 6√2
This simplification is crucial in algebra and calculus for simplifying expressions and solving equations.
2. Operations with Square Roots:
Square roots follow specific rules when performing addition, subtraction, multiplication, and division.
-
Addition/Subtraction: We can only add or subtract square roots with the same radicand (the number under the radical). For example: 2√3 + 5√3 = 7√3. We cannot directly add √2 + √3.
-
Multiplication: To multiply square roots, we multiply the radicands and then simplify: √a × √b = √(ab). For instance, √2 × √8 = √16 = 4.
-
Division: Similar to multiplication, we divide the radicands: √a / √b = √(a/b). For example, √16 / √4 = √4 = 2.
3. Square Roots and Exponents:
Square roots are closely related to exponents. The square root of a number is the same as raising that number to the power of 1/2. Thus, √36 = 36^(1/2) = 6. This relationship extends to other fractional exponents, allowing us to handle more complex calculations involving roots.
Real-World Applications of Square Roots
The concept of the square root, exemplified by finding the positive square root of 36, extends far beyond theoretical mathematics, finding practical application in various fields:
1. Geometry and Trigonometry:
Square roots are indispensable in geometry, particularly when dealing with calculations involving right-angled triangles. The Pythagorean theorem (a² + b² = c²) utilizes square roots to determine the length of the hypotenuse (c) or the lengths of the other sides (a and b) of a right-angled triangle. For example, finding the length of the diagonal of a square with side length 6 involves calculating √(6² + 6²) = √72 = 6√2.
Trigonometry, which studies the relationships between angles and sides of triangles, also heavily relies on square roots. Calculating distances and angles frequently involves applying square root functions.
2. Physics and Engineering:
In physics and engineering, square roots appear in numerous formulas and equations. Calculations related to velocity, acceleration, energy, and forces often involve square roots. For instance, calculating the velocity of an object using kinetic energy involves the square root of a quantity related to mass and energy. Similarly, calculations related to electrical circuits, signal processing, and mechanics frequently employ square roots.
3. Statistics and Probability:
Square roots are essential in statistics and probability. The standard deviation, a measure of the dispersion of data points around the mean, involves the square root of the variance. This measure helps determine the spread or variability within a dataset, which is crucial in various statistical analyses.
4. Computer Graphics and Game Development:
Square roots are fundamental to computer graphics and game development, particularly in rendering 3D environments and calculating distances between objects. The computations involved in translating objects in three-dimensional space frequently involve the square root function. This allows for accurate and realistic representation of graphical scenes.
5. Finance and Investments:
While perhaps less obvious, square roots also play a role in financial calculations. Some financial models involve calculating standard deviations and variances related to investment portfolios, requiring the use of square roots.
Advanced Concepts Related to Square Roots
For those interested in furthering their understanding of square roots, exploring these advanced concepts is beneficial:
1. Complex Numbers:
Extending the concept of square roots to negative numbers introduces complex numbers. The square root of a negative number is an imaginary number, represented by 'i', where i² = -1. For example, √(-9) = 3i. Complex numbers are crucial in advanced mathematics, physics, and electrical engineering.
2. nth Roots:
The concept of square roots can be generalized to nth roots, where we seek a number that, when multiplied by itself 'n' times, equals a given number. For instance, the cube root (3rd root) of 8 is 2, since 2 × 2 × 2 = 8.
3. Numerical Methods for Approximating Square Roots:
For numbers that are not perfect squares, numerical methods like the Babylonian method (also known as Heron's method) provide efficient ways to approximate their square roots to a desired level of accuracy. These iterative methods progressively refine an initial guess to get closer to the actual square root value.
Conclusion
While the positive square root of 36 is simply 6, understanding this seemingly basic concept opens doors to a vast landscape of mathematical possibilities. From the fundamental principles of algebra to the intricate calculations in advanced scientific fields, the square root function plays a crucial, often indispensable, role. This exploration highlights not just the answer to a simple question but the far-reaching implications and practical applications of square roots in various aspects of our world. By grasping the underlying principles and exploring its diverse applications, we gain a deeper appreciation for the power and elegance of this fundamental mathematical concept. Furthermore, understanding the properties and applications of square roots strengthens mathematical skills and provides a valuable foundation for tackling more complex mathematical challenges in various fields.
Latest Posts
Latest Posts
-
What Is The Lcm Of 3 5 And 11
Apr 08, 2025
-
Naming Ionic Compounds With Transition Metals
Apr 08, 2025
-
What Does A Base Feel Like
Apr 08, 2025
-
What Is 3 4 Divided By 2 3 In Fraction Form
Apr 08, 2025
-
How Many Atoms Are In Aluminum
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Positive Square Root Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.