What Is The Lowest Common Multiple Of 7 And 5
listenit
Mar 29, 2025 · 5 min read
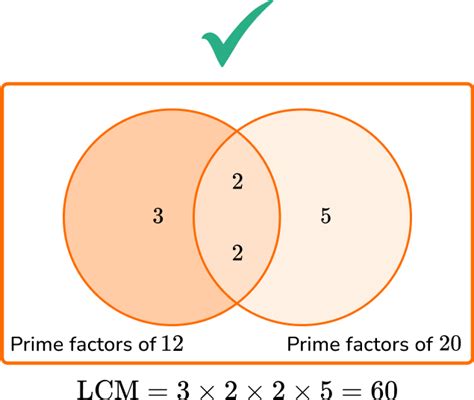
Table of Contents
What is the Lowest Common Multiple (LCM) of 7 and 5? A Deep Dive into Number Theory
Finding the lowest common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to a fascinating world of number theory. This article will not only answer the question "What is the LCM of 7 and 5?" but will also explore the various methods for calculating the LCM, delve into the related concept of the greatest common divisor (GCD), and examine the broader significance of these concepts in mathematics and computer science.
Understanding the Basics: LCM and GCD
Before we tackle the specific case of 7 and 5, let's establish a solid foundation.
What is the Lowest Common Multiple (LCM)? The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Think of it as the smallest common "meeting point" for the multiples of each number.
What is the Greatest Common Divisor (GCD)? The GCD, also known as the greatest common factor (GCF), is the largest positive integer that divides each of the integers without leaving a remainder. It's the largest number that is a factor of all the given numbers.
These two concepts, LCM and GCD, are intimately related. Understanding one often illuminates the other.
Calculating the LCM of 7 and 5: Three Proven Methods
Now, let's address the question at hand: What is the LCM of 7 and 5? We'll explore three common methods to illustrate the versatility of the concept.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list out the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, ...
Notice that the smallest number that appears in both lists is 35. Therefore, the LCM of 7 and 5 is 35.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We first find the prime factorization of each number. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
- Prime factorization of 7: 7 (7 is a prime number itself)
- Prime factorization of 5: 5 (5 is also a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case:
LCM(7, 5) = 7 × 5 = 35
Method 3: Using the GCD
This method leverages the relationship between the LCM and the GCD. The formula connecting LCM and GCD is:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a × b| represents the absolute value of the product of a and b.
First, we need to find the GCD of 7 and 5. Since 7 and 5 are both prime numbers and have no common factors other than 1, their GCD is 1.
Now, we can apply the formula:
LCM(7, 5) = (7 × 5) / 1 = 35
This method confirms our previous results, highlighting the interconnectedness of LCM and GCD.
The Significance of LCM and GCD Beyond Basic Arithmetic
The concepts of LCM and GCD are not merely exercises in elementary number theory; they have significant applications in various fields:
1. Scheduling and Time Management
Imagine you have two machines that run cycles of 7 and 5 hours respectively. To find the time when both machines complete their cycles simultaneously, you need to find the LCM of 7 and 5. The LCM, 35, represents the time in hours when both machines will be at the beginning of their cycles again.
2. Fractions and Least Common Denominator (LCD)
When adding or subtracting fractions, finding the LCD is crucial for simplifying calculations. The LCD is nothing more than the LCM of the denominators. For example, to add 1/7 and 1/5, the LCD is LCM(7, 5) = 35.
3. Computer Science and Algorithms
LCM and GCD are fundamental concepts in several computer science algorithms. For instance, they play a significant role in cryptography, optimization problems, and scheduling tasks in operating systems.
Advanced Concepts and Extensions
The exploration of LCM and GCD extends beyond the simple examples we've explored. More complex scenarios include:
- Finding the LCM of more than two numbers: The same principles apply, although the calculations may become more involved. Prime factorization remains a powerful tool for larger sets of numbers.
- Euclidean algorithm: This efficient algorithm provides a method for finding the GCD of two numbers without relying on prime factorization. This is particularly useful for very large numbers where prime factorization becomes computationally expensive.
- Modular arithmetic: LCM and GCD have significant roles in modular arithmetic, a branch of number theory that deals with remainders. This has applications in cryptography and computer security.
Conclusion: A Simple Problem with Profound Implications
The seemingly simple question of finding the LCM of 7 and 5 has led us on a journey through fundamental number theory concepts. We've discovered three different methods for calculating the LCM, explored its relationship to the GCD, and touched upon its wide-ranging applications in various fields. Understanding LCM and GCD is not just about mastering arithmetic; it's about developing a deeper appreciation for the underlying structure and beauty of mathematics. These concepts form building blocks for more advanced mathematical explorations, impacting fields far beyond the classroom. Remember that a thorough understanding of these basic concepts provides a robust foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
45 Of What Number Is 90
Apr 01, 2025
-
2 And 1 3 As An Improper Fraction
Apr 01, 2025
-
Gcf Of 42 126 And 210
Apr 01, 2025
-
What Are The First 5 Multiples Of 7
Apr 01, 2025
-
What Is 8 10 As A Decimal
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 7 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
