What Is The Lcm Of 3 And 2
listenit
May 25, 2025 · 5 min read
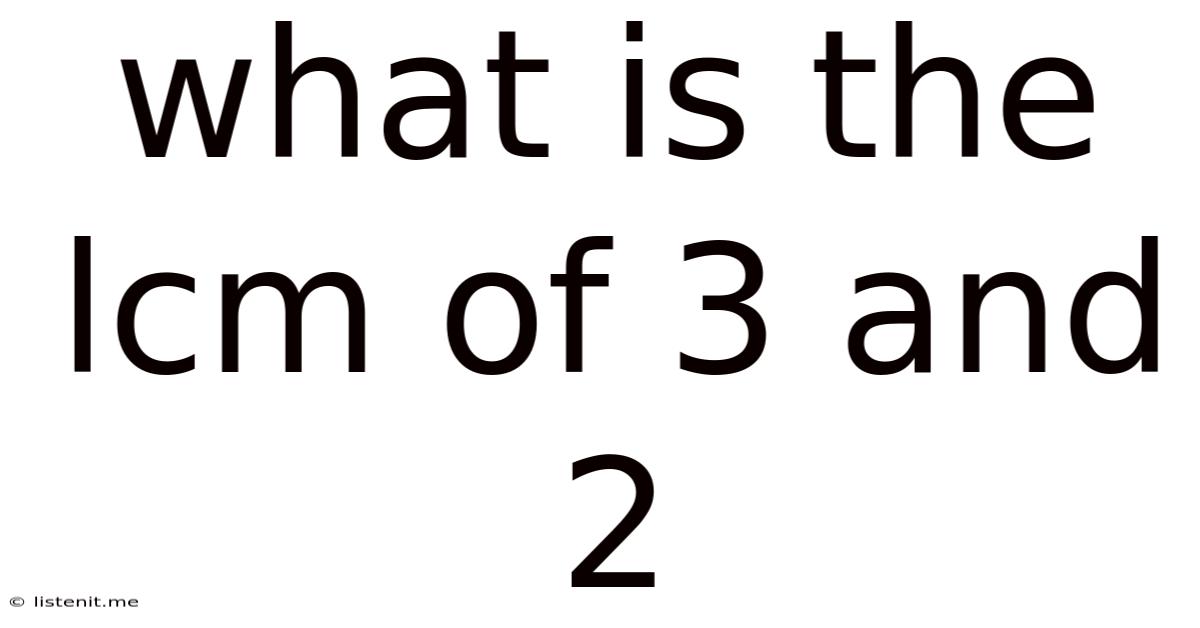
Table of Contents
What is the LCM of 3 and 2? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in arithmetic and number theory with widespread applications in various fields, from scheduling to music theory. This article will comprehensively explore the LCM of 3 and 2, providing a detailed explanation of the process and illustrating its relevance through examples and applications. We’ll go beyond a simple answer and delve into the underlying mathematical principles, exploring different methods for calculating LCMs and highlighting their practical significance.
Understanding Least Common Multiples (LCM)
Before we determine the LCM of 3 and 2, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of all the given numbers.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24... The multiples of 6 are 6, 12, 18, 24, 30... The common multiples of 4 and 6 are 12, 24, 36, and so on. The smallest of these common multiples is 12, therefore, the LCM of 4 and 6 is 12.
Calculating the LCM of 3 and 2: Methods and Explanation
Now, let's tackle the LCM of 3 and 2. Several methods can be used to determine the LCM, each offering a slightly different approach:
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 3 and 2, is listing the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 2: 2, 4, 6, 8, 10, 12...
Observing the lists, we can see that the smallest number appearing in both lists is 6. Therefore, the LCM of 3 and 2 is 6.
Method 2: Prime Factorization
This method is particularly useful when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 2: 2 (2 is a prime number)
Since 3 and 2 are both prime numbers and distinct, the LCM is simply the product of these prime factors: 3 * 2 = 6.
Method 3: Using the Formula (LCM and GCD Relationship)
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers. First, we need to find the GCD of 3 and 2. The GCD is the greatest number that divides both 3 and 2 without leaving a remainder. In this case, the GCD(3, 2) = 1 (since 1 is the only common divisor).
Now, we can use the formula:
LCM(3, 2) * GCD(3, 2) = 3 * 2 LCM(3, 2) * 1 = 6 LCM(3, 2) = 6
Applications of LCM: Real-World Examples
The concept of LCM extends beyond abstract mathematical exercises; it finds practical applications in various real-world scenarios:
1. Scheduling and Time Management
Imagine you have two tasks: one repeats every 3 days, and another repeats every 2 days. To find out when both tasks will coincide again, you need to find the LCM of 3 and 2. The LCM is 6, meaning both tasks will occur on the same day every 6 days.
2. Music Theory
LCM plays a crucial role in music theory, specifically in determining the least common denominator for rhythmic patterns. Consider two musical phrases with durations represented by fractions. The LCM of the denominators helps determine the smallest common unit of time for these phrases to synchronize.
3. Fractions and Arithmetic Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to obtain a common denominator. This simplifies the calculation and ensures accurate results. For example, adding 1/3 and 1/2 requires finding the LCM of 3 and 2 (which is 6), and then rewriting the fractions with a denominator of 6 before adding them.
4. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is used to calculate gear ratios. Understanding the LCM helps determine the optimal gear combinations for smooth and efficient power transmission in machines.
5. Cyclic Events
Whenever events repeat cyclically, the LCM determines when these cycles will align. This is useful in various fields, such as predicting planetary alignments in astronomy or understanding recurring patterns in biological systems.
Expanding on LCM: Multiple Numbers
The concept of LCM can be extended to more than two numbers. For example, to find the LCM of 3, 2, and 4, we can use the prime factorization method:
- Prime factorization of 3: 3
- Prime factorization of 2: 2
- Prime factorization of 4: 2²
The LCM is constructed by taking the highest power of each prime factor present: 2² * 3 = 12. Therefore, the LCM of 3, 2, and 4 is 12.
Conclusion: The Significance of LCM
The seemingly simple problem of finding the LCM of 3 and 2 serves as a gateway to understanding a fundamental mathematical concept with far-reaching applications. This article has explored different methods for calculating the LCM and showcased its practical relevance in diverse fields. Mastering the concept of LCM is crucial for success in various areas, from solving basic arithmetic problems to tackling complex engineering challenges. By grasping the principles underlying LCM calculations, you equip yourself with a powerful tool for problem-solving and a deeper understanding of the interconnectedness of mathematical concepts. Remember, understanding the 'why' behind the calculation is just as important as knowing the 'how.' This deeper understanding provides a strong foundation for tackling more advanced mathematical concepts in the future.
Latest Posts
Latest Posts
-
How Many Hours Have I Lived
May 25, 2025
-
What Percent Is 19 Out Of 22
May 25, 2025
-
How Many Square Feet Does A 14000 Btu Ac Cool
May 25, 2025
-
How Many Steps Is 100 Feet
May 25, 2025
-
Can You Give Me The Number To
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.