What Is The Lcm Of 24 And 36
listenit
Mar 30, 2025 · 5 min read
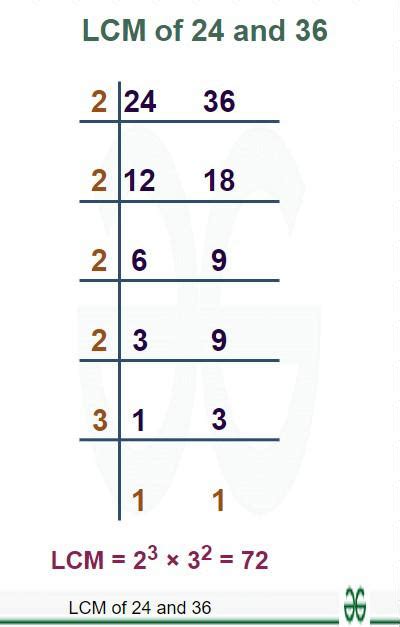
Table of Contents
What is the LCM of 24 and 36? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation opens doors to more advanced mathematical concepts and problem-solving skills. This article will delve into finding the LCM of 24 and 36, exploring various approaches, and explaining the significance of LCMs in various applications.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 24 and 36, let's solidify the definition. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers as factors.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 24 and 36
There are several ways to calculate the LCM of 24 and 36. Let's explore the most common methods:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144...
- Multiples of 36: 36, 72, 108, 144...
Notice that 72 appears in both lists. Therefore, the LCM of 24 and 36 is 72. While simple, this method becomes less efficient with larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors.
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3¹
- Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
To find the LCM using prime factorization:
- Identify the highest power of each prime factor present in the factorizations. In this case, the highest power of 2 is 2³ and the highest power of 3 is 3².
- Multiply these highest powers together. 2³ x 3² = 8 x 9 = 72
Therefore, the LCM of 24 and 36 is 72. This method is more efficient than the listing method, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) of two numbers are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula:
LCM(a, b) = (a x b) / GCD(a, b)
First, let's find the GCD of 24 and 36 using the Euclidean algorithm:
- Divide the larger number (36) by the smaller number (24): 36 ÷ 24 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (12): 24 ÷ 12 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 12.
Now, we can calculate the LCM:
LCM(24, 36) = (24 x 36) / 12 = 864 / 12 = 72
This method is also efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
Understanding LCMs is crucial in various mathematical and real-world applications:
1. Fraction Arithmetic
LCMs are fundamental in adding and subtracting fractions with different denominators. To add or subtract fractions, we need to find a common denominator, and the least common denominator is the LCM of the individual denominators.
For example, to add 1/24 + 1/36, we find the LCM of 24 and 36, which is 72. We then rewrite the fractions with the common denominator:
(3/72) + (2/72) = 5/72
2. Scheduling Problems
LCMs are frequently used in scheduling problems. For example, if two buses depart from the same station at different intervals, the LCM of those intervals will determine when both buses will depart simultaneously again.
Imagine bus A departs every 24 minutes and bus B departs every 36 minutes. The LCM of 24 and 36 (72 minutes) indicates that both buses will depart at the same time again after 72 minutes, or 1 hour and 12 minutes.
3. Music Theory
In music theory, LCMs play a role in determining the least common period of two or more musical rhythms. Understanding the LCM helps to find the points where different rhythmic patterns coincide.
4. Gear Ratios
In mechanics, understanding LCM helps in calculating gear ratios and determining when gears will align perfectly in a system with multiple gears having different numbers of teeth.
5. Cyclic Processes
In various cyclic processes, whether in nature or technology, LCMs help to determine the timing of recurring events.
Conclusion: The Power of LCM
The LCM of 24 and 36 is 72. While this seemingly simple calculation might appear insignificant, the concept of LCM extends far beyond this basic example. Understanding LCMs provides a crucial foundation for more advanced mathematical concepts and is vital in solving real-world problems across diverse fields. Mastering various methods for finding the LCM empowers you to tackle more complex problems efficiently and effectively. From simplifying fractions to solving complex scheduling issues, the least common multiple proves to be a powerful tool in the mathematical toolkit. The methods described here – listing multiples, prime factorization, and the GCD method – provide different approaches to finding the LCM, allowing you to select the most suitable method depending on the context and the complexity of the numbers involved. Remember to practice these methods to solidify your understanding and enhance your problem-solving abilities.
Latest Posts
Latest Posts
-
What Transition Metals Have A Fixed Charge
Apr 01, 2025
-
What Are Biotic Factors And Abiotic Factors
Apr 01, 2025
-
Common Multiples Of 4 And 9
Apr 01, 2025
-
How Many Quarts In 5 Gallon Bucket
Apr 01, 2025
-
What Is The Decimal For 11 20
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 24 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
