What Is The Improper Fraction Of 2 1 2
listenit
Mar 28, 2025 · 5 min read
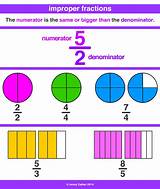
Table of Contents
What is the Improper Fraction of 2 1/2? A Comprehensive Guide
Understanding fractions, especially converting between mixed numbers and improper fractions, is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the mixed number 2 1/2 into its improper fraction equivalent. We'll explore the underlying concepts, provide step-by-step instructions, and offer various examples to solidify your understanding. This article aims to be your ultimate resource for mastering this crucial mathematical concept.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion process, let's clarify the definitions of mixed numbers and improper fractions.
Mixed Numbers: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 1/2 is a mixed number; it represents two whole units and one-half of another unit.
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For instance, 5/2 is an improper fraction because the numerator (5) is larger than the denominator (2). Improper fractions represent a value greater than or equal to one.
The conversion between mixed numbers and improper fractions is a crucial skill in various mathematical operations, including addition, subtraction, multiplication, and division of fractions.
Converting 2 1/2 to an Improper Fraction: A Step-by-Step Approach
Converting the mixed number 2 1/2 to an improper fraction involves a straightforward process:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 2, and the denominator of the fraction is 2. Therefore, we multiply 2 * 2 = 4.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1, we get 4 + 1 = 5.
Step 3: Keep the same denominator.
The denominator remains unchanged throughout the conversion process. In this case, the denominator remains 2.
Step 4: Write the result as an improper fraction.
Combining the results from Steps 2 and 3, we obtain the improper fraction 5/2. Therefore, the improper fraction equivalent of 2 1/2 is 5/2.
Visualizing the Conversion: A Pictorial Representation
Imagine you have two and a half pizzas. Each pizza is divided into two equal slices. You have two whole pizzas, each with two slices (2 x 2 = 4 slices), plus one extra half-slice. In total, you have 4 + 1 = 5 slices. Since each pizza has 2 slices, you have 5/2 slices of pizza, representing the improper fraction 5/2. This visual representation helps to solidify the understanding of the conversion process.
Practical Applications: Why is this Conversion Important?
The ability to convert between mixed numbers and improper fractions is essential for various mathematical operations and real-world applications. Here are some examples:
-
Adding and Subtracting Fractions: You cannot directly add or subtract mixed numbers without first converting them to improper fractions. For example, adding 2 1/2 + 1 1/2 requires converting both mixed numbers to improper fractions (5/2 + 3/2) before performing the addition.
-
Multiplying and Dividing Fractions: While it's possible to multiply and divide mixed numbers directly, it's often simpler and less prone to errors to convert them to improper fractions first. This is particularly helpful when dealing with more complex fractions.
-
Solving Equations: Many algebraic equations involve fractions. The ability to convert between mixed numbers and improper fractions is crucial for solving these equations efficiently.
-
Real-world Scenarios: Imagine you're baking a cake that requires 2 1/2 cups of flour. To accurately measure the flour using a measuring cup that measures in fractions, you'd need to understand that 2 1/2 cups is equivalent to 5/2 cups.
More Examples of Mixed Number to Improper Fraction Conversions
Let's practice converting some more mixed numbers into improper fractions:
-
3 2/3: (3 * 3) + 2 = 11. The denominator remains 3. Therefore, 3 2/3 = 11/3.
-
1 1/4: (1 * 4) + 1 = 5. The denominator remains 4. Therefore, 1 1/4 = 5/4.
-
5 3/8: (5 * 8) + 3 = 43. The denominator remains 8. Therefore, 5 3/8 = 43/8.
-
7 1/5: (7 * 5) + 1 = 36. The denominator remains 5. Therefore, 7 1/5 = 36/5.
-
10 2/7: (10 * 7) + 2 = 72. The denominator remains 7. Therefore, 10 2/7 = 72/7.
These examples illustrate the consistent application of the steps outlined earlier. Remember, the core process remains the same regardless of the specific values of the whole number and the fraction.
Converting Improper Fractions Back to Mixed Numbers
It's also important to understand the reverse process: converting an improper fraction back into a mixed number. This involves dividing the numerator by the denominator.
For example, to convert 5/2 back to a mixed number:
-
Divide the numerator (5) by the denominator (2): 5 ÷ 2 = 2 with a remainder of 1.
-
The quotient (2) becomes the whole number.
-
The remainder (1) becomes the numerator of the fraction.
-
The denominator remains the same (2).
Therefore, 5/2 = 2 1/2.
Mastering Fractions: A Crucial Mathematical Skill
The ability to comfortably convert between mixed numbers and improper fractions is a fundamental skill in mathematics. It underpins many other mathematical operations and has practical applications in various real-world scenarios. By understanding the concepts and practicing the conversion process, you'll build a strong foundation in fractions, making it easier to tackle more complex mathematical problems in the future. Regular practice is key to mastering this essential skill. Remember to visualize the process and use real-world examples to reinforce your understanding. The more you practice, the more confident and proficient you will become.
Latest Posts
Latest Posts
-
What Number Is 60 Of 145
Mar 31, 2025
-
The Ability Of An Organism To Survive And Reproduce
Mar 31, 2025
-
What Is A Master Level Clinician
Mar 31, 2025
-
Religion In The Colony Of Virginia
Mar 31, 2025
-
Titrate Weak Acid With Strong Base
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Improper Fraction Of 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
