What Is The Highest Common Factor Of 28 And 70
listenit
May 24, 2025 · 5 min read
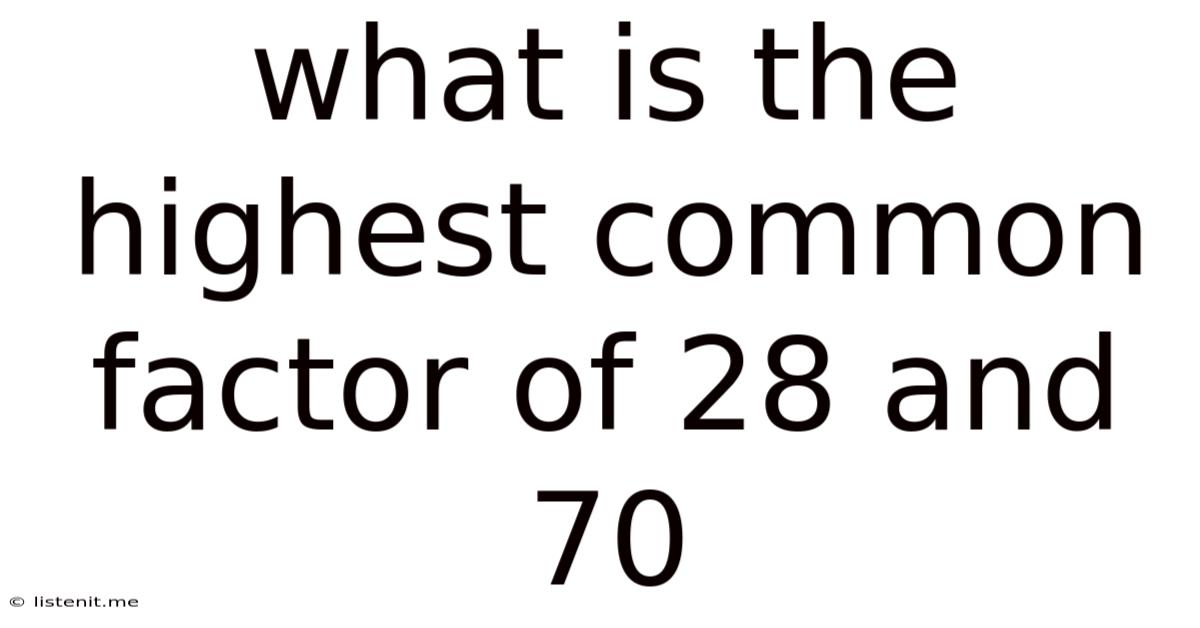
Table of Contents
What is the Highest Common Factor (HCF) of 28 and 70? A Deep Dive into Number Theory
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory. This seemingly simple calculation underlies many more complex mathematical operations and has practical applications in various fields. This article will explore the HCF of 28 and 70, examining different methods to arrive at the solution and delve into the broader significance of this mathematical concept.
Understanding the Highest Common Factor (HCF)
Before we tackle the specific problem of finding the HCF of 28 and 70, let's solidify our understanding of the concept itself. The HCF of two or more numbers is the largest number that divides each of them without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6, therefore, the HCF of 12 and 18 is 6.
Key takeaways about HCF:
- Divisibility: The HCF must divide both numbers completely.
- Largest Common Factor: It's the greatest of all the common factors.
- Uniqueness: For any pair of numbers, there's only one HCF.
- Applications: HCF has applications in simplifying fractions, solving problems related to measurement, and even in cryptography.
Method 1: Prime Factorization Method
This is a classic and widely used method for finding the HCF. It involves breaking down each number into its prime factors and then identifying the common factors. Let's apply this to our problem: finding the HCF of 28 and 70.
1. Prime Factorization of 28:
28 can be expressed as a product of its prime factors as follows:
28 = 2 x 2 x 7 = 2² x 7
2. Prime Factorization of 70:
Similarly, let's find the prime factorization of 70:
70 = 2 x 5 x 7
3. Identifying Common Prime Factors:
Now, we compare the prime factorizations of 28 and 70:
28 = 2² x 7 70 = 2 x 5 x 7
The common prime factors are 2 and 7.
4. Calculating the HCF:
To find the HCF, we multiply the common prime factors together:
HCF(28, 70) = 2 x 7 = 14
Therefore, the highest common factor of 28 and 70 is 14.
Method 2: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the HCF.
Let's apply the Euclidean algorithm to find the HCF of 28 and 70:
- Start with the larger number (70) and the smaller number (28):
70 and 28
- Divide the larger number by the smaller number and find the remainder:
70 ÷ 28 = 2 with a remainder of 14
- Replace the larger number with the smaller number and the smaller number with the remainder:
28 and 14
- Repeat the process:
28 ÷ 14 = 2 with a remainder of 0
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 14.
Therefore, the Euclidean algorithm confirms that the HCF of 28 and 70 is 14.
Method 3: Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor. While simple for smaller numbers, it becomes less efficient as the numbers get larger.
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70
Common Factors: 1, 2, 7, 14
Highest Common Factor: 14
The Significance of HCF in Mathematics and Beyond
The seemingly simple task of finding the HCF has far-reaching implications across various mathematical and practical domains. Here are some key examples:
1. Simplifying Fractions:
The HCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, you divide both the numerator and the denominator by their HCF. For instance, to simplify the fraction 28/70, we find the HCF (which is 14), and divide both the numerator and the denominator by 14, resulting in the simplified fraction 2/5.
2. Solving Measurement Problems:
Imagine you have two pieces of ribbon, one measuring 28 cm and the other 70 cm. You want to cut them into smaller pieces of equal length without any waste. The HCF (14 cm) determines the longest possible length for the smaller pieces.
3. Number Theory and Cryptography:
HCF is fundamental in number theory, providing a basis for understanding concepts like modular arithmetic and prime factorization. These concepts have crucial applications in cryptography, which relies on the difficulty of factoring large numbers to secure communication and data.
4. Computer Science:
Algorithms for computing the HCF are important in computer science for various applications, including data compression and image processing. The efficiency of these algorithms directly impacts the speed and performance of computer programs.
Conclusion: The Power of Simple Concepts
The determination of the highest common factor, while seemingly a straightforward arithmetic task, represents a cornerstone concept in mathematics. Understanding the HCF and mastering various calculation methods, such as prime factorization and the Euclidean algorithm, unlocks the ability to approach a wide array of problems in mathematics, science, and computer science. The HCF's practical applications highlight how even fundamental mathematical ideas can be incredibly powerful tools. This article has explored different ways to calculate the HCF of 28 and 70, demonstrating the consistent result: 14. Further exploration into number theory will only deepen the appreciation for the significance and pervasiveness of this essential mathematical concept.
Latest Posts
Latest Posts
-
6 1 8 As An Improper Fraction
May 24, 2025
-
What Is 3 5 Of 350 000
May 24, 2025
-
Greatest Common Factor Of 45 And 63
May 24, 2025
-
How Many Days Has It Been Since September 19
May 24, 2025
-
Find The Value Of In The Triangle Shown Below
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is The Highest Common Factor Of 28 And 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.