What Is The Greatest Common Factor Of 8 And 28
listenit
May 25, 2025 · 5 min read
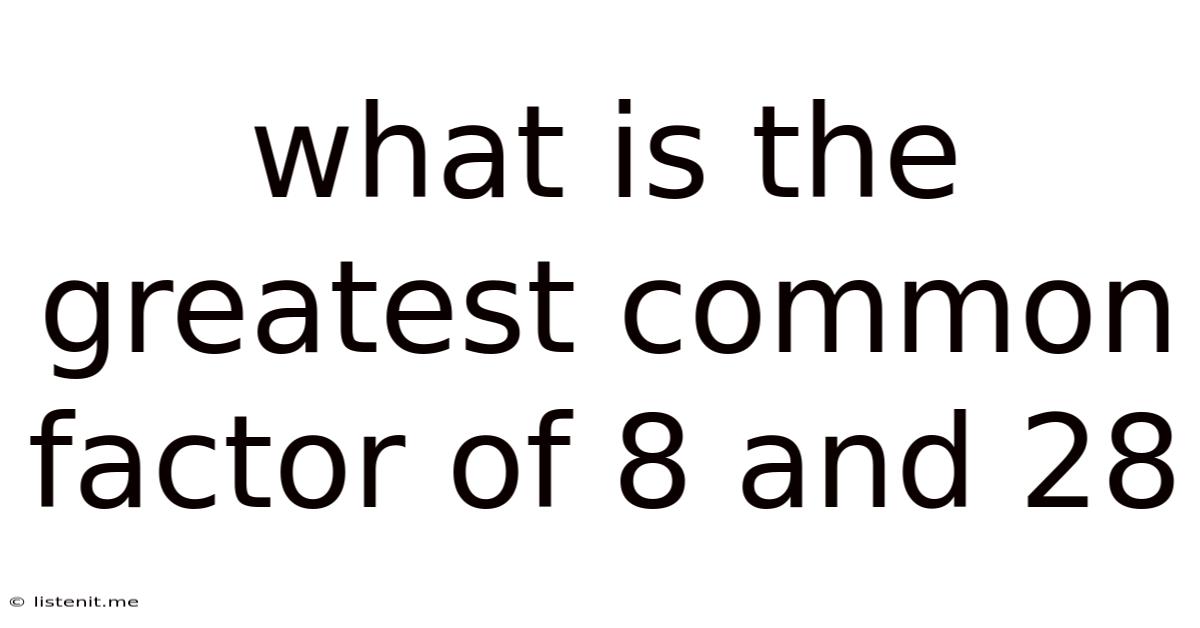
Table of Contents
What is the Greatest Common Factor of 8 and 28? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide will not only answer the question "What is the greatest common factor of 8 and 28?" but also explore the various methods to find the GCF, delve into the importance of GCF in various mathematical applications, and offer practical examples to solidify your understanding.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory with wide-ranging applications in algebra, geometry, and other areas of mathematics. Understanding the GCF is crucial for simplifying fractions, solving equations, and working with various mathematical problems.
The Prime Factorization Method
One of the most reliable methods for finding the GCF is through prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to our problem: finding the GCF of 8 and 28.
- Prime factorization of 8: 8 = 2 x 2 x 2 = 2³
- Prime factorization of 28: 28 = 2 x 2 x 7 = 2² x 7
Now, we identify the common prime factors and their lowest powers. Both 8 and 28 share two factors of 2 (2²). Therefore, the greatest common factor of 8 and 28 is 2 x 2 = 4.
Therefore, the GCF of 8 and 28 is 4.
The Euclidean Algorithm Method
The Euclidean algorithm provides an alternative, efficient way to find the GCF, especially for larger numbers. This method involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 8 and 28:
- Divide the larger number (28) by the smaller number (8): 28 ÷ 8 = 3 with a remainder of 4.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
Again, the GCF of 8 and 28 is 4.
Practical Applications of GCF
The GCF has numerous practical applications across various mathematical fields and real-world scenarios. Here are a few examples:
Simplifying Fractions
The GCF plays a vital role in simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, consider the fraction 28/8. Since the GCF of 28 and 8 is 4, we can simplify the fraction as follows:
28/8 = (28 ÷ 4) / (8 ÷ 4) = 7/2
This simplification makes the fraction easier to understand and work with.
Solving Equations
GCF is essential in solving various algebraic equations, especially those involving factoring. For instance, when factoring quadratic equations, finding the GCF of the coefficients can help simplify the expression and make it easier to find the roots.
Geometry and Measurement
GCF finds applications in geometry problems related to area, volume, and measurement. For example, when determining the dimensions of the largest square tile that can perfectly cover a rectangular floor, the GCF of the floor's length and width provides the side length of the tile.
Real-World Applications
Beyond theoretical mathematics, GCF finds practical use in various real-world scenarios:
- Dividing objects equally: Imagine you have 28 apples and 8 oranges and want to divide them into equal groups without any leftovers. The GCF (4) tells you that you can create 4 equal groups.
- Resource allocation: In resource management, GCF can help distribute resources fairly among different groups or individuals.
- Construction and design: GCF is utilized in construction and design to determine optimal dimensions for materials and spaces.
Exploring Other Methods for Finding GCF
While prime factorization and the Euclidean algorithm are the most common methods, other techniques can be employed to find the GCF, particularly for smaller numbers:
Listing Factors Method
This straightforward method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 8: 1, 2, 4, 8 Factors of 28: 1, 2, 4, 7, 14, 28
The common factors are 1, 2, and 4. The largest among them is 4, confirming that the GCF of 8 and 28 is 4. This method is suitable for smaller numbers but becomes less practical for larger numbers.
Venn Diagram Method
A Venn diagram can visually represent the factors of each number, making it easy to identify the common factors. Draw two overlapping circles, one for each number, list the factors in each circle, and the common factors will be in the overlapping region. The largest factor in the overlapping region is the GCF.
Expanding the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 8, 28, and 12:
-
Prime Factorization:
- 8 = 2³
- 28 = 2² x 7
- 12 = 2² x 3
The common prime factor is 2, and its lowest power is 2². Therefore, the GCF of 8, 28, and 12 is 4.
-
Euclidean Algorithm (extended): You can apply the Euclidean algorithm iteratively to find the GCF of multiple numbers. First, find the GCF of two numbers, then find the GCF of the result and the third number, and so on.
Conclusion: Mastering GCF for Mathematical Proficiency
Finding the greatest common factor is a fundamental skill in mathematics with numerous practical applications. Understanding the different methods – prime factorization, the Euclidean algorithm, listing factors, and using Venn diagrams – equips you with the tools to tackle GCF problems efficiently. Whether simplifying fractions, solving equations, or tackling real-world problems, mastering the concept of GCF enhances your mathematical proficiency and problem-solving abilities. Remember to choose the method most suitable for the numbers involved, and practice regularly to build your understanding and fluency. The GCF, seemingly a simple concept, is a powerful tool in the world of mathematics.
Latest Posts
Latest Posts
-
9 30 To 1 30 How Many Hours
May 26, 2025
-
9 4 5 As An Improper Fraction
May 26, 2025
-
Least Common Multiple Of 2 3 4
May 26, 2025
-
What Is The Greatest Common Factor Of 5 And 20
May 26, 2025
-
What Is The Prime Factorization 24
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 8 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.