What Is The Greatest Common Factor Of 60 And 72
listenit
May 11, 2025 · 5 min read
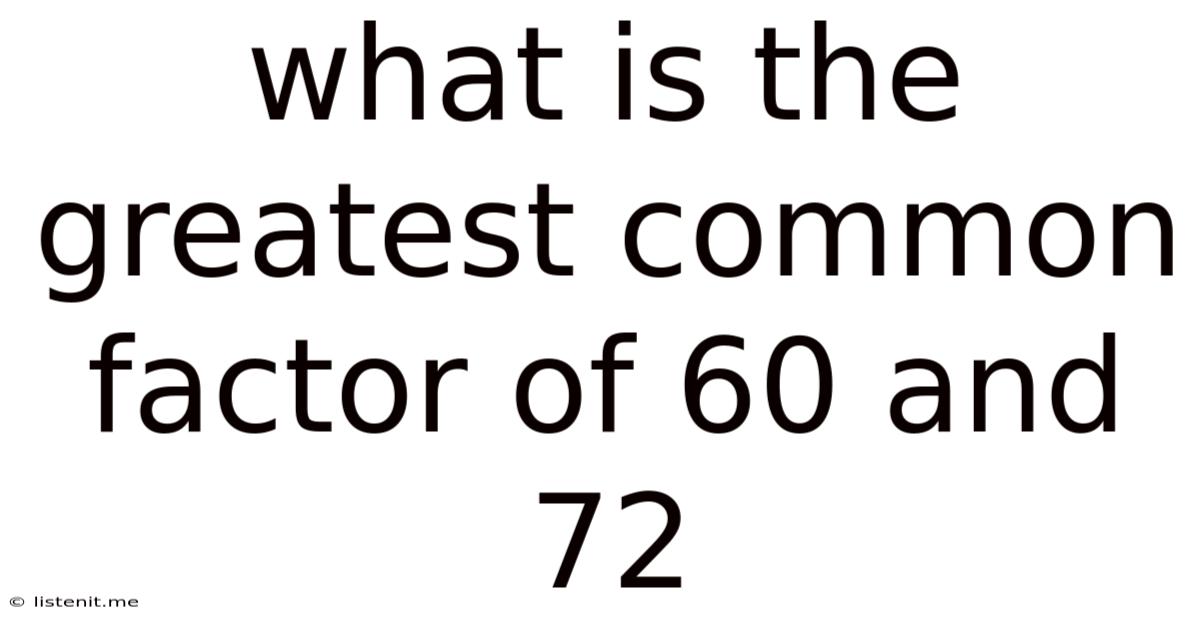
Table of Contents
What is the Greatest Common Factor (GCF) of 60 and 72? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with applications across various fields, from simplifying fractions to solving complex algebraic equations. This article will explore different methods to determine the GCF of 60 and 72, delve into the underlying mathematical principles, and demonstrate the practical relevance of this concept.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
This seemingly simple concept has far-reaching implications in mathematics and beyond. Understanding GCFs allows us to simplify fractions to their lowest terms, solve problems in algebra and geometry, and even contributes to more advanced concepts in cryptography and computer science.
Methods to Find the GCF of 60 and 72
Several methods can be employed to find the GCF of 60 and 72. Let's explore the most common ones:
1. Listing Factors Method
This is a straightforward method, especially suitable for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Comparing the two lists, we observe that the common factors are 1, 2, 3, 4, 6, and 12. The largest of these common factors is 12. Therefore, the GCF of 60 and 72 is 12.
This method works well for smaller numbers but becomes less efficient as the numbers increase in size. Finding all the factors of very large numbers can be time-consuming.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization of a number is its expression as a product of prime numbers.
Prime Factorization of 60:
60 = 2 × 30 = 2 × 2 × 15 = 2 × 2 × 3 × 5 = 2² × 3 × 5
Prime Factorization of 72:
72 = 2 × 36 = 2 × 2 × 18 = 2 × 2 × 2 × 9 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 60 and 72 have 2 and 3 as prime factors. The lowest power of 2 is 2¹ (or 2) and the lowest power of 3 is 3¹. Therefore, the GCF is 2 × 3 = 12.
This method is more efficient than listing factors, especially for larger numbers, as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 60 and 72:
- 72 = 60 × 1 + 12 (Subtract 60 from 72, leaving a remainder of 12)
- 60 = 12 × 5 + 0 (Divide 60 by 12, leaving a remainder of 0)
When the remainder is 0, the GCF is the last non-zero remainder, which is 12.
The Euclidean algorithm is particularly efficient for large numbers because it avoids the need to find all factors. It's the preferred method for computer algorithms that need to calculate GCFs quickly.
Applications of GCF
The concept of the greatest common factor extends far beyond simple number theory. Here are some practical applications:
-
Simplifying Fractions: To reduce a fraction to its simplest form, we divide both the numerator and denominator by their GCF. For example, the fraction 60/72 can be simplified to 5/6 by dividing both 60 and 72 by their GCF, which is 12.
-
Solving Algebraic Equations: GCFs are often used in factoring algebraic expressions. Factoring an expression simplifies it and allows for easier manipulation and solution.
-
Geometry: GCFs can be used to find the dimensions of the largest square that can tile a rectangle with given dimensions. The side length of the largest square is the GCF of the rectangle's length and width.
-
Modular Arithmetic: GCFs play a crucial role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Music Theory: GCFs help determine the intervals between musical notes, contributing to the understanding of harmony and composition.
Further Exploration of Number Theory Concepts Related to GCF
Understanding GCF leads to a deeper appreciation of related concepts in number theory, such as:
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the formula: GCF(a, b) × LCM(a, b) = a × b.
-
Coprime Numbers (Relatively Prime Numbers): Two numbers are coprime if their GCF is 1. This means they share no common factors other than 1.
-
Diophantine Equations: These are algebraic equations where only integer solutions are sought. GCFs play a significant role in determining the solvability and the solutions of certain Diophantine equations.
Conclusion: The Significance of GCF
The seemingly simple concept of the greatest common factor has profound implications in various mathematical fields and practical applications. Understanding the different methods for calculating GCF, such as listing factors, prime factorization, and the Euclidean algorithm, equips us to tackle problems involving simplification, factoring, and more advanced mathematical concepts. The GCF of 60 and 72, determined to be 12 through several methods, serves as a concrete example illustrating the power and versatility of this fundamental concept. Its significance extends far beyond simple calculations, providing a cornerstone for more complex mathematical investigations and real-world applications. Mastering this concept opens the door to a deeper understanding of number theory and its pervasive influence on numerous disciplines.
Latest Posts
Latest Posts
-
How Many Grams Is A Pound Of Butter
May 11, 2025
-
The Function Of The Lens Is To
May 11, 2025
-
How To Solve System Of Inequalities Without Graphing
May 11, 2025
-
Can Rate Constant K Be Negative
May 11, 2025
-
7 Protons 7 Neutrons 7 Electrons
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 60 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.