What Is The Greatest Common Factor Of 2 And 4
listenit
May 26, 2025 · 6 min read
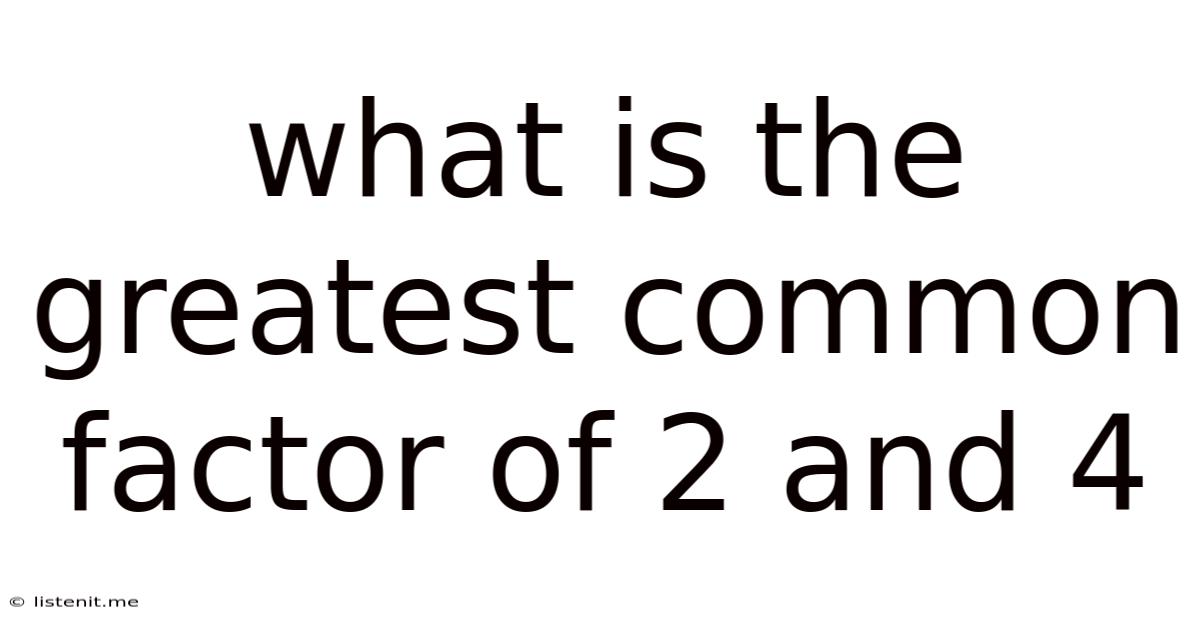
Table of Contents
What is the Greatest Common Factor of 2 and 4? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) might seem like a simple arithmetic problem, especially when dealing with small numbers like 2 and 4. However, understanding the concept of GCF, its applications, and different methods to find it lays a strong foundation in number theory and has far-reaching implications in various fields, from cryptography to computer science. This article will not only answer the question of what the GCF of 2 and 4 is but will also explore the underlying mathematical concepts and provide a detailed explanation of various methods for finding the GCF of any two numbers.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into all the given numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest among these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Why is GCF Important?
The GCF isn't just a theoretical concept; it has practical applications in various areas:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 12/18 can be simplified to 2/3 by dividing both the numerator and the denominator by their GCF, which is 6.
-
Solving Word Problems: Many word problems in mathematics, especially those involving division and sharing, require finding the GCF to find the most efficient or equitable solution.
-
Algebra and Geometry: GCF plays a vital role in factoring algebraic expressions and solving geometric problems related to area and volume calculations.
-
Cryptography: In cryptography, GCF is used in various algorithms, such as the Euclidean algorithm, which is fundamental in public-key cryptography.
-
Computer Science: GCF is used in algorithms for computer-aided design (CAD), image processing, and data compression.
Finding the GCF of 2 and 4
Now, let's address the specific question: What is the greatest common factor of 2 and 4?
The factors of 2 are 1 and 2. The factors of 4 are 1, 2, and 4.
The common factors of 2 and 4 are 1 and 2. The greatest of these common factors is 2.
Therefore, the greatest common factor of 2 and 4 is 2.
Methods for Finding the GCF
While the method of listing factors is suitable for small numbers, it becomes cumbersome for larger numbers. Here are some more efficient methods:
1. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime Factorization of 2: 2 (2 is a prime number)
- Prime Factorization of 4: 2 x 2 = 2²
The common prime factor is 2. The lowest power of 2 is 2¹, which is 2. Therefore, the GCF is 2.
2. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 2 and 4:
- Start with the larger number (4) and the smaller number (2).
- Subtract the smaller number from the larger number: 4 - 2 = 2
- Replace the larger number with the result (2) and keep the smaller number (2). Now we have 2 and 2.
- Since the numbers are equal, the GCF is 2.
The Euclidean algorithm is particularly useful for finding the GCF of larger numbers where the prime factorization method can be more time-consuming.
3. Listing Factors Method (for smaller numbers)
As we demonstrated earlier, listing all the factors of each number and identifying the common factors is a straightforward method, especially when dealing with smaller numbers.
GCF and Least Common Multiple (LCM)
The GCF and the least common multiple (LCM) are closely related concepts. The LCM of two numbers is the smallest positive integer that is divisible by both numbers. There's a useful relationship between the GCF and LCM:
For any two positive integers 'a' and 'b': (a x b) = (GCF(a, b) x LCM(a, b))
This means that the product of two numbers is equal to the product of their GCF and LCM. Let's verify this with the numbers 2 and 4:
- a = 2
- b = 4
- GCF(2, 4) = 2
- LCM(2, 4) = 4
(2 x 4) = (2 x 4) => 8 = 8
The equation holds true, demonstrating the relationship between GCF and LCM.
Applications of GCF in Real-World Scenarios
The applications of GCF extend beyond theoretical mathematics and find practical uses in various real-world situations:
-
Sharing Items Equally: Imagine you have 12 apples and 18 oranges, and you want to distribute them equally among several people without having any leftovers. Finding the GCF (which is 6) tells you that you can distribute the fruits to 6 people equally, giving each person 2 apples and 3 oranges.
-
Cutting Fabric: Suppose you have two pieces of fabric, one measuring 12 meters and the other measuring 18 meters. You want to cut them into equal-sized pieces without wasting any fabric. Finding the GCF (6 meters) tells you the largest size of the pieces you can cut.
-
Arranging Objects in Rows and Columns: If you have 12 squares and you want to arrange them in rows and columns such that the number of rows and columns is the same, you need to find the factors of 12. If you want to find the largest possible square you can create using these squares, you need to find the largest perfect square that is a factor of 12.
Conclusion
The greatest common factor is a fundamental concept in number theory with wide-ranging applications. While finding the GCF of 2 and 4 is a straightforward task, understanding the underlying principles and different methods for calculating the GCF, especially for larger numbers, is crucial for various mathematical and real-world applications. The Euclidean algorithm and prime factorization method provide efficient ways to determine the GCF, and understanding the relationship between GCF and LCM further enhances our understanding of number theory. Mastering this concept builds a strong foundation for more advanced mathematical studies and problem-solving skills. Remember that the ability to efficiently calculate GCF is not just about finding a numerical answer, but it's about the analytical skills and the understanding of core mathematical principles that are developed in the process.
Latest Posts
Latest Posts
-
Vitamin K Functions In The Synthesis Of Prothrombin And
May 27, 2025
-
Will I Lose Weight After H Pylori Treatment
May 27, 2025
-
Carbohydrates Are Composed Of What Elements
May 27, 2025
-
Rhesus Macaques Doing Match To Sample Video
May 27, 2025
-
Does Milk Protein Concentrate Have Lactose
May 27, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 2 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.