What Is The Greatest Common Factor For 24 And 32
listenit
Apr 06, 2025 · 5 min read
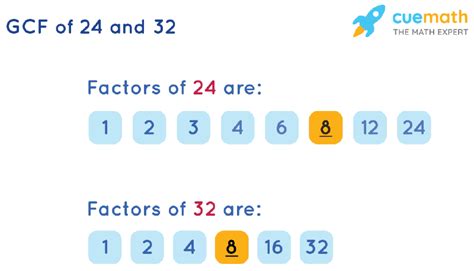
Table of Contents
What is the Greatest Common Factor for 24 and 32? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide delves into the intricacies of determining the GCF for 24 and 32, exploring multiple approaches and their applications. We'll also touch upon the broader significance of GCF in mathematics and real-world scenarios.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory with far-reaching implications in various mathematical fields and practical applications.
Key Concepts:
- Factors: Factors are numbers that divide evenly into a given number. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Common Factors: Common factors are numbers that are factors of two or more numbers. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
- Greatest Common Factor (GCF): The GCF is the largest of the common factors. In our 12 and 18 example, the GCF is 6.
Methods for Finding the GCF of 24 and 32
Let's explore several methods to determine the GCF of 24 and 32. Each method offers unique insights into the concept of divisibility and prime factorization.
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Factors of 32: 1, 2, 4, 8, 16, 32
Common Factors: 1, 2, 4, 8
GCF: 8
This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves expressing each number as a product of its prime factors (factors that are only divisible by 1 and themselves).
Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3 Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
To find the GCF, identify the common prime factors and multiply them together using the lowest power present in either factorization. Both 24 and 32 share three factors of 2.
GCF: 2³ = 8
This method provides a systematic approach, especially useful for numbers with multiple factors.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
- Divide the larger number (32) by the smaller number (24): 32 ÷ 24 = 1 with a remainder of 8.
- Replace the larger number with the remainder (8): Now we find the GCF of 24 and 8.
- Repeat the process: 24 ÷ 8 = 3 with a remainder of 0.
- The GCF is the last non-zero remainder: The last non-zero remainder is 8.
Therefore, the GCF of 24 and 32 is 8.
The Euclidean algorithm is computationally efficient and avoids the need for complete prime factorization, making it a powerful tool for finding the GCF of even very large numbers.
Applications of the Greatest Common Factor
The GCF is not just a theoretical concept; it has various practical applications across several domains:
1. Simplifying Fractions
The GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF.
For example, to simplify the fraction 24/32, we find the GCF of 24 and 32, which is 8. Dividing both the numerator and the denominator by 8 gives us the simplified fraction 3/4.
2. Solving Word Problems
Many word problems involve finding the GCF. For instance, imagine you have 24 apples and 32 oranges, and you want to arrange them into baskets with equal numbers of each fruit in each basket. The GCF (8) represents the maximum number of baskets you can make, with each basket containing 3 apples and 4 oranges.
3. Geometry and Measurement
GCF is essential in geometry when dealing with problems involving area, perimeter, and volume. For example, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the length and width of the floor.
4. Algebra and Polynomials
GCF finds application in simplifying algebraic expressions and factoring polynomials. Finding the GCF of the terms in a polynomial allows for factoring out the common factor, simplifying the expression.
Beyond the Basics: Exploring Further Concepts
While finding the GCF of 24 and 32 is a fundamental exercise, understanding related concepts broadens your mathematical understanding.
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. The GCF and LCM are closely related. The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. This relationship is useful in various mathematical operations.
Relatively Prime Numbers
Two numbers are considered relatively prime or coprime if their GCF is 1. For example, 9 and 10 are relatively prime because their GCF is 1.
Applications in Cryptography
The concept of GCF, particularly the Euclidean algorithm, plays a significant role in modern cryptography. Algorithms like RSA encryption utilize the GCF to ensure secure data transmission.
Conclusion: Mastering GCF for Enhanced Mathematical Proficiency
Understanding the GCF, its various methods of calculation, and its wide range of applications is crucial for anyone seeking to enhance their mathematical proficiency. From simplifying fractions to solving complex word problems and contributing to advanced fields like cryptography, the seemingly simple concept of the greatest common factor holds profound significance in the realm of mathematics and beyond. By mastering these concepts, you'll not only improve your problem-solving skills but also develop a deeper appreciation for the interconnectedness of mathematical ideas. The journey of understanding the GCF of 24 and 32 serves as a stepping stone to exploring more advanced mathematical concepts and their real-world applications. Continue exploring, experimenting, and practicing to unlock the full potential of this fundamental concept.
Latest Posts
Latest Posts
-
Two Different Isotopes Of An Element Have The Same
Apr 08, 2025
-
What Is Between 1 2 And 3 4
Apr 08, 2025
-
Why Is Chemistry Called The Central Science
Apr 08, 2025
-
How Many Electrons In Third Shell
Apr 08, 2025
-
What Does Gravitational Potential Energy Depend On
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor For 24 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.