What Is The Gcf Of 8 And 16
listenit
Apr 08, 2025 · 5 min read
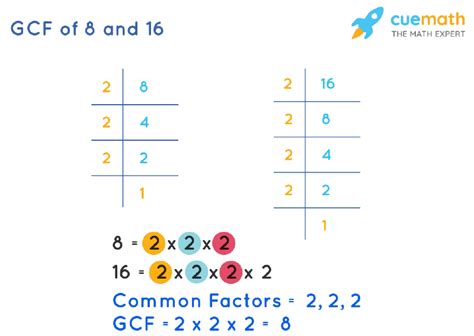
Table of Contents
What is the GCF of 8 and 16? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts unlocks a world of mathematical possibilities. This comprehensive guide will explore the GCF of 8 and 16, delving into various methods for calculation and showcasing its practical applications in different fields. We’ll go beyond a simple answer, providing you with a robust understanding of GCFs and their importance in mathematics.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific case of 8 and 16, let's define what a greatest common factor actually is. The GCF, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
Think of it like finding the largest shared building block of two numbers. Just as you can build structures with various sizes of blocks, numbers are built from their factors. The GCF represents the largest block size that can be used to build both numbers.
Methods for Finding the GCF
Several methods exist for calculating the GCF. Let's examine three common approaches:
1. Listing Factors
This method is particularly useful for smaller numbers. We simply list all the factors of each number and then identify the largest factor they share.
Factors of 8: 1, 2, 4, 8 Factors of 16: 1, 2, 4, 8, 16
Comparing the lists, we see that the common factors are 1, 2, 4, and 8. The largest of these is 8. Therefore, the GCF of 8 and 16 is 8.
2. Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. The GCF is then constructed using the common prime factors.
Prime factorization of 8: 2 x 2 x 2 = 2³ Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
Both numbers share three factors of 2. Therefore, the GCF is 2 x 2 x 2 = 8. This method is more efficient for larger numbers than listing factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
- Divide the larger number (16) by the smaller number (8): 16 ÷ 8 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder (which was implicitly the divisor in the last step), which is 8.
Why is Finding the GCF Important?
Understanding and calculating GCFs isn't just an academic exercise. It has practical applications in various areas:
1. Simplifying Fractions
GCFs are crucial for simplifying fractions to their lowest terms. To simplify a fraction, you divide both the numerator and denominator by their GCF. For example, the fraction 16/8 can be simplified to 2/1 (or simply 2) by dividing both the numerator and denominator by their GCF, which is 8.
2. Solving Word Problems
Many word problems involving sharing or dividing quantities require finding the GCF. For example, imagine you have 16 apples and 8 oranges, and you want to divide them into identical bags without any leftover fruit. The GCF (8) tells you the maximum number of identical bags you can create (each bag containing 2 apples and 1 orange).
3. Geometry and Measurement
GCFs play a significant role in geometry. When finding the dimensions of the largest square that can tile a rectangle, the side length of the square is the GCF of the rectangle's length and width.
4. Algebra and Number Theory
GCFs are fundamental concepts in algebra and number theory, forming the basis for more advanced mathematical operations and theorems.
Beyond the Basics: Exploring Related Concepts
Understanding GCFs opens the door to exploring related concepts:
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is a multiple of each of the integers. While the GCF represents the largest shared factor, the LCM represents the smallest shared multiple. The GCF and LCM are related through the formula: GCF(a, b) x LCM(a, b) = a x b. For 8 and 16, the LCM is 16.
Relatively Prime Numbers
Two numbers are considered relatively prime (or coprime) if their GCF is 1. For example, the numbers 15 and 28 are relatively prime because their GCF is 1.
Practical Applications and Real-World Examples
The applications of GCF extend beyond abstract mathematical concepts:
- Music Theory: GCFs help determine the simplest ratios for musical intervals.
- Construction: Calculating the GCF is essential for determining the dimensions of tiles or bricks to cover a surface efficiently.
- Computer Science: GCFs are used in algorithms for data compression and encryption.
Conclusion: Mastering the GCF
Understanding the concept of the greatest common factor, and the various methods for calculating it, is a foundational skill in mathematics. Whether you're simplifying fractions, solving word problems, or exploring advanced mathematical concepts, mastering the GCF provides a powerful tool for problem-solving and a deeper appreciation of mathematical relationships. The GCF of 8 and 16, as we've shown through various methods, is 8. This seemingly simple calculation unlocks a wealth of possibilities within the broader world of mathematics and its numerous applications. By understanding this fundamental concept, you equip yourself with a crucial skill for various mathematical and real-world challenges.
Latest Posts
Latest Posts
-
What Is The Subject Of A Story
Apr 08, 2025
-
216 To The Power Of 1 3
Apr 08, 2025
-
What Is The Factors For 32
Apr 08, 2025
-
Number Of Valence Electrons For Boron
Apr 08, 2025
-
What Holds Two Strands Of Dna Together
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.