What Is The Exact Value Of Tan 195
listenit
May 11, 2025 · 4 min read
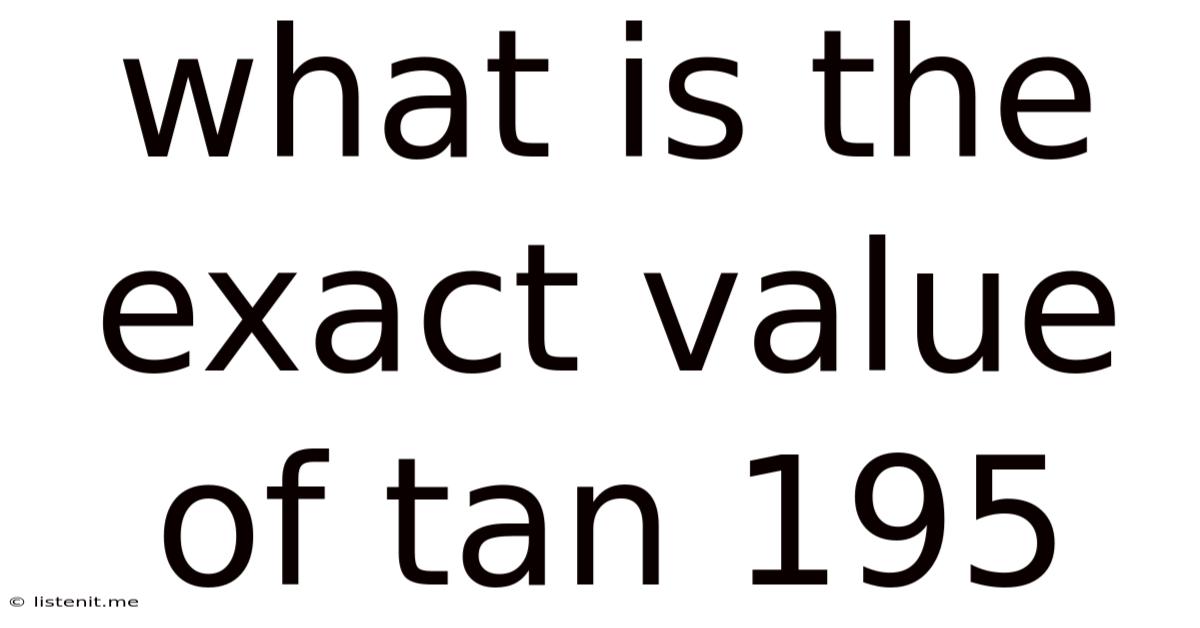
Table of Contents
What is the Exact Value of tan 195°? A Comprehensive Guide
Finding the exact value of trigonometric functions like tan 195° often requires breaking down the angle into simpler, more manageable components. This seemingly complex calculation can be elegantly solved using trigonometric identities and a bit of clever manipulation. Let's delve into the process step-by-step, exploring various methods and solidifying our understanding of trigonometric principles along the way.
Understanding the Problem: tan 195°
Our goal is to determine the exact value of tan 195°, without resorting to a calculator. We'll avoid approximations and focus on deriving an exact, radical expression. 195° isn't one of the standard angles (like 30°, 45°, 60°, etc.) found on the unit circle, making a direct lookup impossible. Instead, we must utilize trigonometric identities and angle addition/subtraction formulas to simplify the expression.
Method 1: Using the Angle Sum/Difference Formula
One powerful approach involves expressing 195° as a sum or difference of angles whose tangent values are known. We can express 195° as:
- 195° = 180° + 15°
- 195° = 225° - 30°
- 195° = 150° + 45°
- 195° = 135° + 60°
While all are valid, let's choose 195° = 180° + 15° for illustrative purposes. This utilizes the tangent addition formula:
tan(A + B) = (tan A + tan B) / (1 - tan A tan B)
In our case, A = 180° and B = 15°. Therefore:
tan 195° = tan (180° + 15°) = (tan 180° + tan 15°) / (1 - tan 180° tan 15°)
We know that tan 180° = 0. This simplifies the equation significantly:
tan 195° = tan 15°
Now we need to find the exact value of tan 15°.
Finding the Exact Value of tan 15°
We can find tan 15° by expressing it as a difference of angles whose tangent values are known:
15° = 45° - 30°
Applying the tangent subtraction formula:
tan(A - B) = (tan A - tan B) / (1 + tan A tan B)
tan 15° = tan (45° - 30°) = (tan 45° - tan 30°) / (1 + tan 45° tan 30°)
We know that tan 45° = 1 and tan 30° = 1/√3 = √3/3. Substituting these values:
tan 15° = (1 - √3/3) / (1 + √3/3)
To rationalize the denominator, multiply the numerator and denominator by 3:
tan 15° = (3 - √3) / (3 + √3)
Further rationalizing by multiplying the numerator and denominator by the conjugate of the denominator (3 - √3):
tan 15° = (3 - √3)² / (9 - 3) = (9 - 6√3 + 3) / 6 = (12 - 6√3) / 6 = 2 - √3
Therefore, tan 195° = tan 15° = 2 - √3
Method 2: Using the Half-Angle Formula
Another effective method utilizes the half-angle formula for tangent:
tan(θ/2) = (1 - cos θ) / sin θ = sin θ / (1 + cos θ)
We can express 195° as half of 390°. Since 390° = 360° + 30°, it's equivalent to 30° in terms of trigonometric values.
Using the second form of the half-angle formula:
tan(195°) = tan(390°/2) = sin 30° / (1 + cos 30°)
Knowing sin 30° = 1/2 and cos 30° = √3/2:
tan 195° = (1/2) / (1 + √3/2) = (1/2) / ((2 + √3)/2) = 1 / (2 + √3)
Rationalizing the denominator by multiplying by the conjugate (2 - √3):
tan 195° = (2 - √3) / (4 - 3) = 2 - √3
This confirms our result from Method 1.
Method 3: Utilizing the Unit Circle and Reference Angles
While less direct than the previous methods, understanding the unit circle and reference angles provides valuable insight. 195° lies in the third quadrant, where both sine and cosine are negative. Its reference angle is 195° - 180° = 15°.
Therefore, tan 195° will be positive (negative/negative) and equal in magnitude to tan 15°. We've already calculated tan 15° to be 2 - √3.
Verifying the Result
The consistency across different methods strongly supports our conclusion. We've independently derived the exact value of tan 195° as 2 - √3 using three distinct approaches: the angle sum/difference formula, the half-angle formula, and analysis using the unit circle and reference angles. This reinforces our understanding and confidence in the result.
Practical Applications and Further Exploration
Understanding how to derive exact trigonometric values is crucial in various fields:
- Calculus: Exact values are essential when dealing with derivatives and integrals of trigonometric functions. Approximations can introduce significant errors.
- Physics and Engineering: Many physical phenomena are modeled using trigonometric functions. Accurate calculations are critical for precise predictions and designs.
- Computer Graphics and Game Development: Accurate trigonometric calculations are fundamental for rendering 3D graphics and simulations.
Conclusion: The Exact Value of tan 195°
The exact value of tan 195° is definitively 2 - √3. This comprehensive exploration involved multiple methods, highlighting the power and elegance of trigonometric identities. Understanding these methods not only provides a solution but also strengthens your grasp of fundamental trigonometric concepts, proving invaluable in numerous applications. Remember to always check your work using different methods to ensure accuracy and solidify your understanding of the underlying principles. This detailed approach emphasizes the importance of precise calculations beyond simple approximations, leading to a more robust and accurate understanding of trigonometric functions.
Latest Posts
Latest Posts
-
Is This A Pronoun Or Adjective
May 12, 2025
-
Height Of A Isosceles Triangle Formula
May 12, 2025
-
What Is The Name Of Hclo3
May 12, 2025
-
How To Write 0 8 As A Fraction
May 12, 2025
-
Round To The Nearest Cent Example
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Exact Value Of Tan 195 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.