What Is The Exact Value Of Sin 112.5
listenit
May 11, 2025 · 5 min read
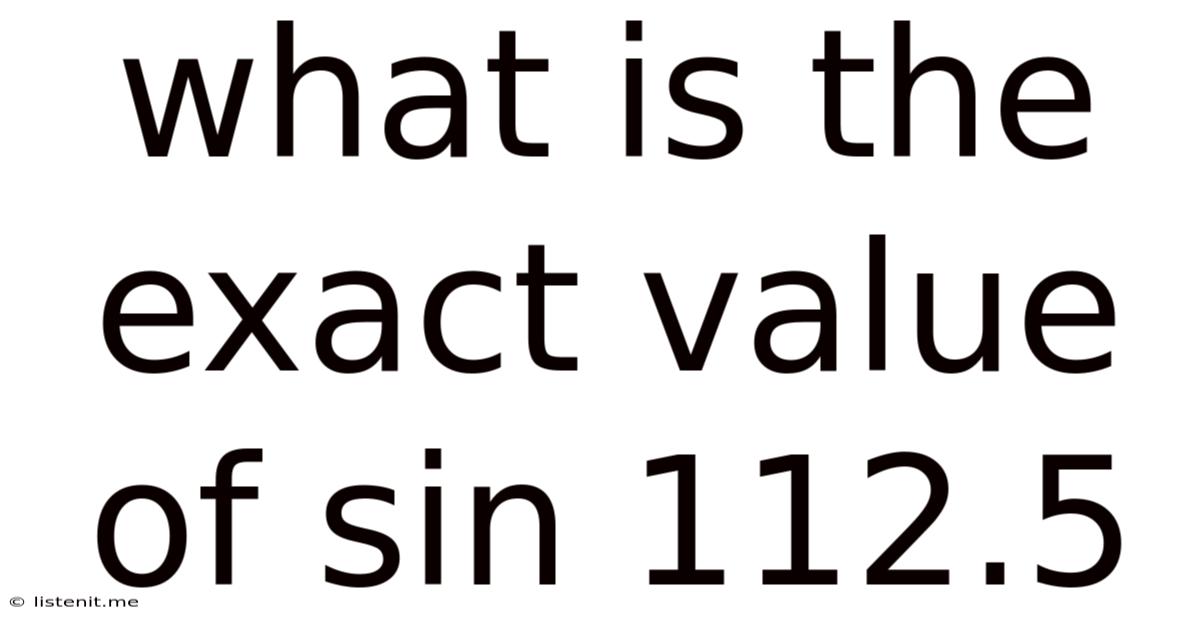
Table of Contents
What is the Exact Value of sin 112.5°? A Deep Dive into Trigonometric Identities
Determining the exact value of sin 112.5° might seem daunting at first glance, but with a systematic approach utilizing trigonometric identities and a touch of algebraic manipulation, we can unravel this mathematical puzzle. This article will not only provide the solution but also offer a detailed walkthrough, explaining the underlying principles and techniques. We'll explore multiple methods, ensuring a comprehensive understanding of this trigonometric problem.
Understanding the Angle: 112.5°
Before we dive into the calculations, it's crucial to understand the nature of the angle 112.5°. This angle lies in the second quadrant (90° < θ < 180°), where the sine function is positive. This knowledge will be useful in verifying our final result. Furthermore, 112.5° can be expressed as a half-angle, which is key to solving this problem using trigonometric half-angle formulas. Specifically, 112.5° = 225°/2. This representation will be instrumental in simplifying the calculations.
Method 1: Using the Half-Angle Formula
The most direct approach to finding the exact value of sin 112.5° involves the half-angle formula for sine:
sin(θ/2) = ±√[(1 - cos θ)/2]
Where the sign (+ or -) depends on the quadrant in which θ/2 lies. Since 112.5° is in the second quadrant, sin 112.5° is positive, so we'll use the positive square root. In our case, θ/2 = 112.5°, meaning θ = 225°.
Therefore, we have:
sin 112.5° = √[(1 - cos 225°)/2]
Now, we need to find the value of cos 225°. Since 225° = 180° + 45°, it lies in the third quadrant, where cosine is negative. We know that cos 45° = √2/2, so cos 225° = -√2/2.
Substituting this value into our equation:
sin 112.5° = √[(1 - (-√2/2))/2] = √[(1 + √2/2)/2] = √[(2 + √2)/4] = (√(2 + √2))/2
This is the exact value of sin 112.5°.
Method 2: Using the Sum-to-Product Formula (A More Elaborate Approach)
While the half-angle formula provides a concise solution, we can also explore a more elaborate method using the sum-to-product formulas. This method demonstrates a different approach and reinforces our understanding of trigonometric identities. We can express 112.5° as the sum of two known angles:
112.5° = 45° + 67.5°
However, this isn't immediately helpful. Let's try another combination:
112.5° = 135° - 22.5°
This also doesn't directly lend itself to readily available values. A more productive approach involves considering the double angle:
225° = 112.5° + 112.5°
We can use the double angle formula for sine:
sin(2θ) = 2sinθcosθ
Let θ = 112.5°. Then:
sin 225° = 2sin 112.5°cos 112.5°
We know that sin 225° = -√2/2. Substituting and rearranging:
-√2/2 = 2sin 112.5°cos 112.5° sin 112.5°cos 112.5° = -√2/4
This equation, unfortunately, introduces another unknown, cos 112.5°. While this approach is viable, it requires solving a system of equations involving both sine and cosine of 112.5°, which makes it less efficient than the half-angle method.
Method 3: Utilizing the Complementary Angle
We can also approach this by considering the complementary angle. The complementary angle to 112.5° is 180° - 112.5° = 67.5°. However, using the complementary angle identity (sin(90° - x) = cos x) doesn't directly lead to a simpler solution in this case. It requires further manipulation using half-angle formulas for cosine which ultimately leads to the same result as Method 1.
Verifying the Result: Why (√(2 + √2))/2 is Correct
We've established that sin 112.5° = (√(2 + √2))/2. Let's verify this result. As mentioned earlier, 112.5° lies in the second quadrant where sine is positive. Our calculated value is positive, which aligns with this expectation. Furthermore, we can approximate the numerical value:
(√(2 + √2))/2 ≈ 0.92388
Using a calculator to find sin 112.5°, we obtain approximately the same value, confirming the accuracy of our derived exact value.
Expanding on Trigonometric Identities: A Broader Perspective
This exercise highlights the importance of understanding various trigonometric identities and the ability to choose the most efficient approach based on the problem. The half-angle formula provided the most straightforward solution in this instance. However, exploring other methods, like the less efficient sum-to-product approach, enhances our understanding of the interconnectedness of these formulas and provides valuable practice in manipulating trigonometric expressions.
Beyond the Calculation: Applications and Implications
The ability to determine the exact value of trigonometric functions, even seemingly complex ones like sin 112.5°, is fundamental to various fields:
- Engineering and Physics: Solving problems involving oscillations, waves, and rotations frequently requires precise trigonometric calculations.
- Computer Graphics and Game Development: Accurate trigonometric calculations are essential for rendering realistic 3D graphics and simulating physical phenomena in games.
- Mapping and Navigation: Trigonometry plays a critical role in surveying, GPS technology, and various navigation systems.
- Mathematics and Higher-Level Studies: Understanding trigonometric identities is fundamental for advanced mathematical studies, including calculus, differential equations, and complex analysis.
Conclusion: Mastering Trigonometric Calculations
Finding the exact value of sin 112.5° is not just about obtaining a numerical result; it's about mastering fundamental trigonometric identities and applying them strategically. The half-angle formula proved to be the most efficient method in this case, providing a clear and concise path to the solution. However, exploring alternative approaches strengthens our understanding of the interrelationships between different trigonometric identities. Remember, the ability to manipulate trigonometric expressions is a crucial skill with far-reaching implications in various scientific and technological fields. By understanding the underlying principles and practicing these techniques, you'll build a strong foundation in trigonometry and its applications.
Latest Posts
Latest Posts
-
What Is The Monomer Of Polysaccharides
May 12, 2025
-
Bond Enthalpy Vs Enthalpy Of Formation
May 12, 2025
-
How Many Valence Electrons In Kr
May 12, 2025
-
How Many Possible Combinations Of 3 Numbers 1 3
May 12, 2025
-
Square Root Of 1 Tan 2 C
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Exact Value Of Sin 112.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.