What Is The Derivative Of 6/x
listenit
May 11, 2025 · 5 min read
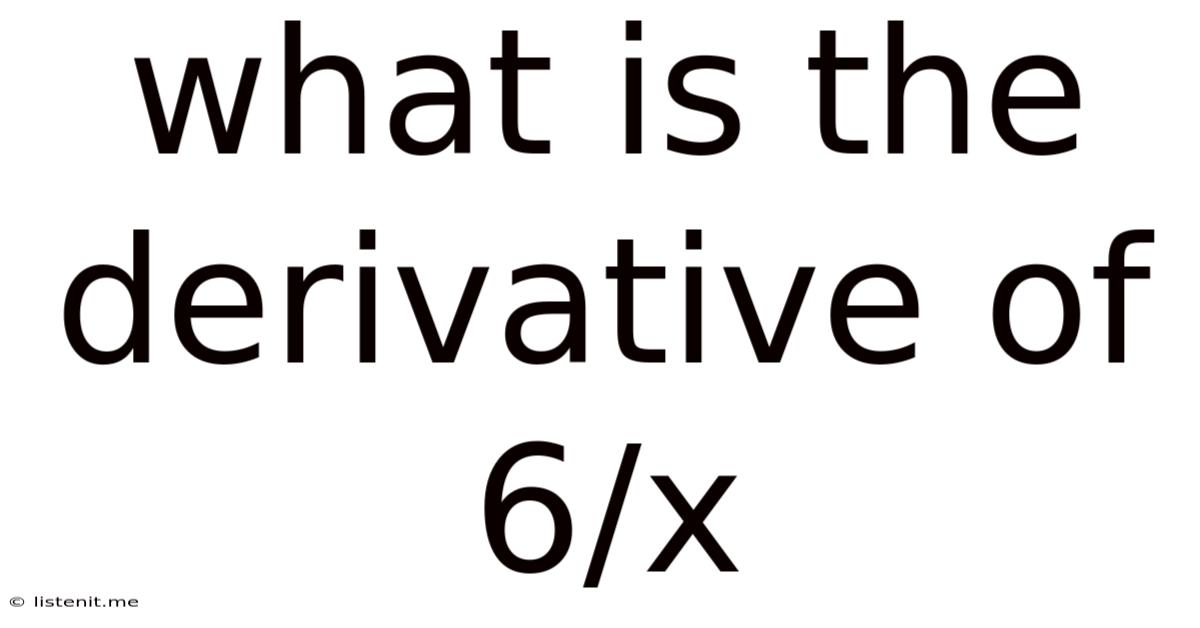
Table of Contents
What is the Derivative of 6/x? A Comprehensive Guide
Finding the derivative of functions is a cornerstone of calculus. This guide will delve into the process of deriving the derivative of 6/x, exploring various approaches and providing a comprehensive understanding of the underlying concepts. We'll cover the power rule, the quotient rule, and even explore the connection to limits, ensuring a thorough grasp of this seemingly simple yet fundamentally important problem.
Understanding the Power Rule
Before diving into the specifics of 6/x, let's refresh our understanding of the power rule, a fundamental tool for finding derivatives. The power rule states that the derivative of x<sup>n</sup> is nx<sup>n-1</sup>, where 'n' is any real number. This seemingly simple rule is the foundation for differentiating a vast array of functions.
For example:
- The derivative of x² is 2x (n=2, so 2x<sup>2-1</sup> = 2x).
- The derivative of x³ is 3x² (n=3, so 3x<sup>3-1</sup> = 3x²).
- The derivative of x<sup>-1</sup> is -x<sup>-2</sup> (n=-1, so -1x<sup>-1-1</sup> = -x<sup>-2</sup>).
This last example is particularly relevant to our problem, as 6/x can be rewritten in a form suitable for the power rule.
Rewriting 6/x using Exponential Notation
To apply the power rule effectively, we must rewrite 6/x as an exponential function. Recall that 1/x is equivalent to x<sup>-1</sup>. Therefore, 6/x can be expressed as 6x<sup>-1</sup>. This simple rewriting is crucial for applying the power rule.
Applying the Power Rule to 6x<sup>-1</sup>
Now that we've expressed 6/x as 6x<sup>-1</sup>, applying the power rule becomes straightforward. Remember the power rule: the derivative of x<sup>n</sup> is nx<sup>n-1</sup>. In our case, n = -1, and the coefficient is 6.
Therefore:
d/dx (6x<sup>-1</sup>) = 6 * (-1)x<sup>-1-1</sup> = -6x<sup>-2</sup>
This simplifies to:
-6/x²
Therefore, the derivative of 6/x is -6/x².
Understanding the Result: The Negative Sign and the x² in the Denominator
The negative sign in the derivative signifies a decreasing function. As x increases, the value of 6/x decreases, and the derivative reflects this negative rate of change.
The x² in the denominator indicates that the rate of change decreases as x increases. The further you move away from the origin along the x-axis, the shallower the slope of the curve 6/x becomes.
Alternative Approach: The Quotient Rule
While the power rule is the most efficient method for this specific problem, it's also beneficial to understand how the quotient rule would be applied. The quotient rule is used to find the derivative of a function that is a ratio of two other functions. It's defined as:
d/dx (u/v) = (v(du/dx) - u(dv/dx)) / v²
where 'u' and 'v' are functions of x.
In our case, u = 6 and v = x. Therefore:
- du/dx = 0 (the derivative of a constant is always zero)
- dv/dx = 1 (the derivative of x is 1)
Applying the quotient rule:
d/dx (6/x) = (x(0) - 6(1)) / x² = -6/x²
As you can see, the quotient rule yields the same result: -6/x²
Connecting to Limits: The Definition of the Derivative
At its core, the derivative is defined using limits. The derivative of a function f(x) at a point x is defined as:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
Applying this definition to f(x) = 6/x:
f'(x) = lim (h→0) [ (6/(x + h) - 6/x) / h ]
This expression can be simplified through algebraic manipulation, involving finding a common denominator and eventually canceling out the 'h' in the denominator. This process would lead to the same result: -6/x². While more complex, understanding the limit definition reinforces the conceptual foundation of the derivative.
Practical Applications and Real-World Examples
The derivative of 6/x, and the broader concept of derivatives, has numerous practical applications across various fields:
-
Physics: Calculating rates of change, such as velocity (the derivative of position with respect to time) or acceleration (the derivative of velocity with respect to time). Imagine analyzing the movement of a particle whose position is described by a function involving 6/x.
-
Economics: Determining marginal cost, marginal revenue, or marginal profit. These concepts represent the rate of change of cost, revenue, or profit with respect to the quantity produced or sold. A function similar to 6/x might model aspects of production or pricing.
-
Engineering: Optimizing designs or processes. Derivatives are crucial in finding maximums and minimums, leading to optimized designs in structural engineering, circuit design, and many other fields.
-
Computer Science: In machine learning and artificial intelligence, derivatives are fundamental to optimization algorithms, like gradient descent, which helps refine models and improve their accuracy.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, here are some areas for further exploration:
-
Higher-order derivatives: The second derivative (the derivative of the derivative), third derivative, and so on. These higher-order derivatives provide information about the concavity and other properties of the function.
-
Derivatives of more complex functions: Understanding how to derive functions involving combinations of functions, such as products, compositions, or implicit functions.
-
Partial derivatives: For functions of multiple variables, partial derivatives allow you to examine the rate of change with respect to each variable independently.
-
Applications in differential equations: Derivatives are the foundation of differential equations, which are powerful tools for modeling a wide range of phenomena in science and engineering.
Conclusion
Finding the derivative of 6/x, while seemingly a simple task, provides a solid foundation for understanding core calculus concepts. Through applying the power rule, the quotient rule, and even referencing the limit definition, we've demonstrated different approaches to arrive at the correct solution: -6/x². This seemingly simple derivative has far-reaching implications in numerous fields, highlighting the importance of mastering these fundamental principles of calculus. Understanding this derivative opens the door to further exploration of more complex functions and applications.
Latest Posts
Latest Posts
-
What Does Light Travel Fastest Through Solid Liquid Or Gas
May 12, 2025
-
A Major Function Of The Cell Membrane Is To
May 12, 2025
-
What Is The Square Root Of 185
May 12, 2025
-
1 Mole Of Hydrogen In Grams
May 12, 2025
-
Whats The Prime Factorization Of 30
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of 6/x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.