What Is Half Of 5 5/8
listenit
May 24, 2025 · 5 min read
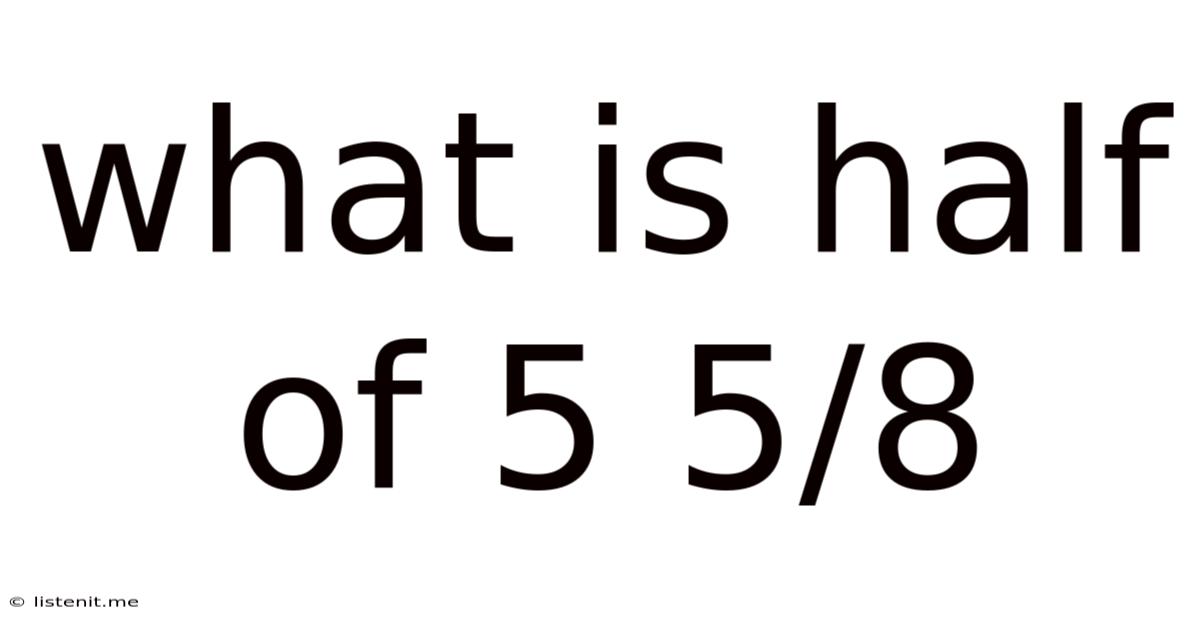
Table of Contents
What is Half of 5 5/8? A Deep Dive into Fractions and Beyond
Finding half of a mixed number like 5 5/8 might seem like a simple arithmetic problem, but it provides a fantastic opportunity to explore fundamental mathematical concepts and brush up on essential fraction skills. This article will not only solve the problem but will also delve into the underlying principles, offering various approaches to tackle similar problems and expanding your understanding of fractions in general.
Understanding Mixed Numbers and Fractions
Before jumping into the calculation, let's solidify our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, such as 5 5/8. This represents 5 whole units plus an additional 5/8 of a unit. A fraction, on the other hand, represents a part of a whole, expressed as a numerator (top number) over a denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Converting Mixed Numbers to Improper Fractions
To easily work with mixed numbers, especially when performing operations like finding half, it's often beneficial to convert them into improper fractions. An improper fraction has a numerator that is greater than or equal to its denominator. To convert 5 5/8 into an improper fraction:
- Multiply the whole number by the denominator: 5 * 8 = 40
- Add the numerator: 40 + 5 = 45
- Keep the same denominator: The denominator remains 8.
Therefore, 5 5/8 is equivalent to the improper fraction 45/8.
Calculating Half of 5 5/8
Now that we've converted 5 5/8 to an improper fraction, finding half becomes a simple matter of division. To find half of 45/8, we divide by 2, or equivalently, multiply by 1/2:
(45/8) / 2 = (45/8) * (1/2) = 45/16
This improper fraction, 45/16, represents the answer, but it's usually more convenient to express it as a mixed number.
Converting Improper Fractions to Mixed Numbers
To convert 45/16 back to a mixed number:
- Divide the numerator by the denominator: 45 ÷ 16 = 2 with a remainder of 13.
- The quotient becomes the whole number: The whole number is 2.
- The remainder becomes the numerator of the fraction: The numerator is 13.
- Keep the same denominator: The denominator remains 16.
Therefore, 45/16 is equivalent to the mixed number 2 13/16.
So, half of 5 5/8 is 2 13/16.
Alternative Methods: A Step-by-Step Approach
While the method above is efficient, let's explore a more step-by-step approach that might be easier to grasp for beginners:
- Find half of the whole number: Half of 5 is 2.5 or 2 1/2.
- Find half of the fraction: Half of 5/8 is (5/8) / 2 = 5/16.
- Combine the results: Add the two halves together: 2 1/2 + 5/16. To add these, we need a common denominator:
- Convert 2 1/2 to an improper fraction: (2 * 2 + 1) / 2 = 5/2
- Find a common denominator for 5/2 and 5/16 (which is 16):
- 5/2 * 8/8 = 40/16
- Add the fractions: 40/16 + 5/16 = 45/16
- Convert the improper fraction back to a mixed number: 45/16 = 2 13/16
This method demonstrates the same result but breaks down the process into smaller, more manageable steps.
Practical Applications and Real-World Examples
Understanding fractions and mixed numbers is crucial in numerous real-world scenarios:
- Cooking and Baking: Recipes often involve fractions and mixed numbers for precise ingredient measurements. Knowing how to halve a recipe is essential.
- Construction and Engineering: Precise measurements are critical in these fields, requiring a solid understanding of fractions for accurate calculations.
- Sewing and Crafting: Patterns and measurements frequently involve fractions and mixed numbers.
- Financial Calculations: Dealing with percentages, interest rates, and other financial aspects often involves fractional calculations.
Expanding Your Knowledge: Working with More Complex Fractions
This problem serves as a foundation for understanding more complex fraction operations. Let's briefly touch upon some related concepts:
- Adding and Subtracting Fractions: This involves finding a common denominator and then adding or subtracting the numerators.
- Multiplying Fractions: This involves multiplying the numerators and multiplying the denominators.
- Dividing Fractions: This involves inverting the second fraction and then multiplying.
- Simplifying Fractions: This involves reducing a fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor.
Mastering these operations will equip you to handle more challenging problems involving fractions and mixed numbers.
Conclusion: Beyond the Calculation
While the answer to "What is half of 5 5/8?" is 2 13/16, the true value lies in the process of arriving at that answer. This problem provided an opportunity to review and reinforce fundamental mathematical concepts related to fractions and mixed numbers. By understanding the underlying principles and exploring different approaches, you've not only solved the problem but also broadened your mathematical skills, equipping you to tackle similar problems with confidence and ease. Remember, the journey of learning is continuous, and each problem solved opens doors to further mathematical exploration and understanding. Continue practicing, exploring different methods, and building your confidence in working with fractions – a skill that will serve you well in many aspects of life.
Latest Posts
Latest Posts
-
What Day Of The Week Is April 13 2024
May 24, 2025
-
What Is The Tax On 100
May 24, 2025
-
How To Calculate Z Score On Calculator
May 24, 2025
-
3 Is 1 Of What Amount
May 24, 2025
-
400 Sq In To Sq Ft
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 5 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.