What Is Half Of 5 1/2
listenit
May 22, 2025 · 5 min read
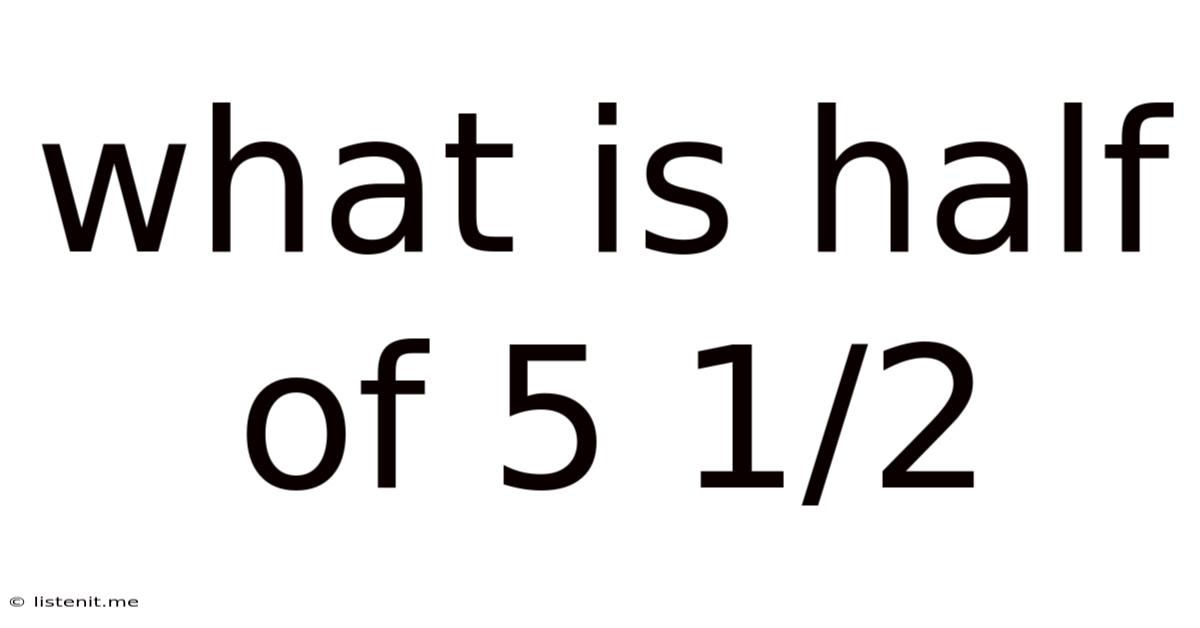
Table of Contents
What is Half of 5 1/2? A Deep Dive into Fractions and Their Applications
The seemingly simple question, "What is half of 5 1/2?" opens a door to a fascinating world of fractions, their manipulation, and their practical applications in everyday life. While the answer itself is straightforward, understanding the underlying concepts provides a solid foundation for more complex mathematical operations. This article will not only answer the question but explore the various methods for solving it, delve into the significance of fractions, and showcase their relevance in diverse fields.
Understanding Fractions: A Foundation for Calculation
Before we tackle the problem at hand, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
For instance, in the fraction 1/2, the denominator (2) signifies that the whole is divided into two equal parts, and the numerator (1) represents one of those parts. Understanding this basic concept is crucial for working with fractions effectively.
Methods for Calculating Half of 5 1/2
There are several approaches to calculating half of 5 1/2. Let's explore the most common and efficient methods:
Method 1: Converting to an Improper Fraction
This is arguably the most straightforward method. We begin by converting the mixed number 5 1/2 into an improper fraction. To do this, we multiply the whole number (5) by the denominator (2) and add the numerator (1). This result (11) becomes the new numerator, while the denominator remains the same (2). Therefore, 5 1/2 is equivalent to 11/2.
Now, to find half of 11/2, we simply multiply it by 1/2:
(11/2) * (1/2) = 11/4
Finally, we convert the improper fraction 11/4 back into a mixed number by dividing the numerator (11) by the denominator (4). This gives us 2 with a remainder of 3. Therefore, the answer is 2 3/4.
Method 2: Working with the Whole Number and Fraction Separately
This method involves splitting the problem into two parts: finding half of the whole number (5) and half of the fraction (1/2) separately, then adding the results.
Half of 5 is simply 5/2 = 2.5.
Half of 1/2 is (1/2) * (1/2) = 1/4.
Adding these together: 2.5 + 0.25 = 2.75, which is equivalent to 2 3/4.
Method 3: Decimal Conversion
We can also convert the mixed number 5 1/2 into a decimal: 5.5. Then, we simply divide 5.5 by 2:
5.5 / 2 = 2.75
This decimal, 2.75, is equivalent to the fraction 2 3/4.
The Significance of Fractions in Various Fields
The ability to work with fractions is fundamental to numerous fields, extending far beyond the classroom:
1. Cooking and Baking: Recipes often call for fractional amounts of ingredients (e.g., 1/2 cup of sugar, 2/3 cup of flour). Accurate fractional calculations are essential for achieving the desired results.
2. Construction and Engineering: Precise measurements are crucial in construction and engineering. Fractions are used extensively in blueprints, calculations for materials, and ensuring structural integrity. Understanding fractions is vital for accurate estimations and preventing errors.
3. Finance and Business: Fractions are commonly used in financial calculations, including calculating interest rates, discounts, profit margins, and stock prices. Accurate fractional understanding is key to making sound financial decisions.
4. Science and Technology: Scientific measurements often involve fractions and decimals. In fields like chemistry and physics, precise calculations using fractions are essential for experiments and research.
5. Music: Musical notation frequently employs fractions to represent time signatures and note durations. Understanding fractions is necessary for accurate music reading and composition.
Beyond the Basics: Expanding Fractional Knowledge
While calculating half of 5 1/2 might seem elementary, mastering fractions lays a groundwork for more complex mathematical concepts:
-
Algebra: Solving algebraic equations often involves manipulating fractions.
-
Calculus: Calculus extensively utilizes fractions and their derivatives.
-
Probability and Statistics: Fractions are fundamental to expressing probabilities and interpreting statistical data.
-
Geometry: Calculating areas, volumes, and angles often requires fractional computations.
Practical Applications and Real-World Examples
Let's consider some real-world scenarios where understanding fractions and calculating half of 5 1/2 becomes relevant:
-
Sharing Resources: Imagine you have 5 1/2 pizzas to share equally among four people. Knowing that half of 5 1/2 is 2 3/4 means each person receives 2 3/4 pizzas.
-
Measuring Ingredients: If a recipe calls for 5 1/2 cups of flour and you want to halve the recipe, you'll need 2 3/4 cups of flour.
-
Dividing a Task: If a project takes 5 1/2 hours to complete, and you want to split the work equally between two people, each person will spend 2 3/4 hours on the task.
-
Calculating Costs: If an item costs $5.50 and you receive a 50% discount, the discounted price will be $2.75.
These examples demonstrate the practical application of understanding fractions in everyday life.
Conclusion: Mastering Fractions – A Lifelong Skill
The seemingly simple question of finding half of 5 1/2 provides a valuable opportunity to explore the world of fractions and their significance. From basic arithmetic to complex scientific calculations, the ability to manipulate fractions remains a crucial skill throughout life. By understanding the various methods for solving such problems and appreciating their applications in diverse fields, we can enhance our mathematical prowess and effectively tackle various real-world challenges. So, next time you encounter a fractional calculation, remember the power and versatility of these seemingly small numbers. Mastering fractions is not just about getting the right answer; it's about unlocking a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
Can Drug Use Cause Multiple Sclerosis
Jun 05, 2025
-
What Does Elevation Of The Left Hemidiaphragm Mean
Jun 05, 2025
-
Does Fasting Kill Parasites In The Body
Jun 05, 2025
-
Average Size Of Spleen In Cm
Jun 05, 2025
-
Pancreas Is Obscured By Overlying Bowel Gas
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 5 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.