What Is A Factor Pair Of 32
listenit
Mar 29, 2025 · 6 min read
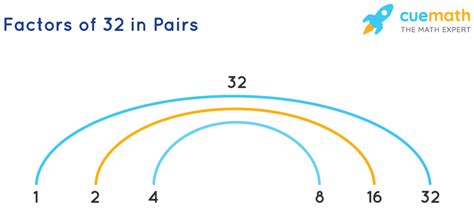
Table of Contents
What is a Factor Pair of 32? A Deep Dive into Number Theory
Understanding factor pairs is fundamental to grasping core concepts in number theory and algebra. This comprehensive guide will explore the concept of factor pairs, focusing specifically on the factor pairs of 32. We'll delve into definitions, methods for finding factor pairs, and applications of this knowledge in various mathematical contexts. We'll also explore the broader implications of factor pairs within the world of mathematics.
Defining Factors and Factor Pairs
Before diving into the factor pairs of 32, let's establish clear definitions.
Factors: A factor of a number is any integer that divides the number evenly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides 12 without leaving a remainder.
Factor Pairs: A factor pair is a set of two factors whose product equals a given number. Crucially, factor pairs always consist of two numbers. For instance, the factor pairs of 12 are (1, 12), (2, 6), and (3, 4). Notice that (4,3) is considered the same factor pair as (3,4) - order doesn't matter.
Finding the Factor Pairs of 32: A Systematic Approach
To find all the factor pairs of 32, we can employ several methods. The most straightforward method involves systematically testing integers to see if they divide 32 without leaving a remainder.
-
Start with 1: 1 is always a factor of any positive integer. Its pair is 32 (because 1 x 32 = 32). So, our first factor pair is (1, 32).
-
Check 2: 32 is an even number, so 2 is a factor. 32 divided by 2 is 16, giving us the factor pair (2, 16).
-
Check 3: 32 is not divisible by 3 (32 divided by 3 leaves a remainder).
-
Check 4: 32 divided by 4 is 8, resulting in the factor pair (4, 8).
-
Check 5: 32 is not divisible by 5.
-
Check 6: 32 is not divisible by 6.
-
Check 7: 32 is not divisible by 7.
-
Check 8: We've already found 8 as a factor in the pair (4,8). We’ve reached a point where we’ve covered all pairs. This illustrates an important point: When working our way up, you only need to check up to the square root of the number. The square root of 32 is approximately 5.66. Once we reach a number greater than the square root, its pair will have already been discovered.
Therefore, the complete list of factor pairs for 32 is:
- (1, 32)
- (2, 16)
- (4, 8)
Visualizing Factor Pairs: Prime Factorization and Factor Trees
Another helpful technique for finding factor pairs is prime factorization. Prime factorization involves expressing a number as a product of its prime factors. A prime factor is a number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
The prime factorization of 32 is 2 x 2 x 2 x 2 x 2, or 2<sup>5</sup>. This prime factorization helps us understand the building blocks of 32 and systematically derive its factors. From the prime factorization, we can easily construct the factor pairs:
- 2<sup>0</sup> x 2<sup>5</sup> = 1 x 32 = 32
- 2<sup>1</sup> x 2<sup>4</sup> = 2 x 16 = 32
- 2<sup>2</sup> x 2<sup>3</sup> = 4 x 8 = 32
A factor tree can visually represent this process:
32
/ \
2 16
/ \
2 8
/ \
2 4
/ \
2 2
By combining the prime factors in different ways, you systematically obtain all factors and, subsequently, the factor pairs.
Applications of Factor Pairs: Beyond Basic Number Theory
The concept of factor pairs extends far beyond simple exercises in number theory. Understanding factor pairs is crucial in several mathematical areas and real-world applications:
-
Algebraic Factoring: Factoring algebraic expressions relies heavily on understanding factors. For example, factoring the quadratic expression x² + 5x + 6 involves finding two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term). These numbers form a factor pair of 6, which are 2 and 3. Therefore, the expression factors as (x + 2)(x + 3).
-
Finding the Greatest Common Factor (GCF): The GCF of two or more numbers is the largest number that divides all of them evenly. Finding the GCF often involves identifying common factors, which are directly related to factor pairs. For instance, to find the GCF of 32 and 48, we'd look at their factor pairs. 32 has factors 1, 2, 4, 8, 16, 32. 48 has factors 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. The greatest common factor is 16.
-
Finding the Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of all the given numbers. Understanding factors and factor pairs can aid in calculating the LCM efficiently, particularly when dealing with larger numbers.
-
Simplifying Fractions: Factor pairs are invaluable when simplifying fractions. By identifying common factors in the numerator and denominator, you can reduce a fraction to its simplest form.
-
Solving Equations: In certain types of equations, particularly those involving quadratic expressions, knowledge of factors and factor pairs is essential for solving for the unknown variable.
Expanding the Concept: Exploring Factor Pairs of Other Numbers
To solidify understanding, let's briefly explore finding factor pairs for other numbers.
Factor Pairs of 24:
The prime factorization of 24 is 2³ x 3. This yields the following factor pairs:
- (1, 24)
- (2, 12)
- (3, 8)
- (4, 6)
Factor Pairs of 100:
The prime factorization of 100 is 2² x 5². The factor pairs are:
- (1, 100)
- (2, 50)
- (4, 25)
- (5, 20)
- (10, 10)
Conclusion: The Significance of Factor Pairs in Mathematics
Factor pairs, while seemingly simple, are a fundamental concept underpinning many areas of mathematics. From basic arithmetic to advanced algebraic manipulations, understanding how to identify and utilize factor pairs is crucial for success. The ability to efficiently find factor pairs empowers problem-solving in various mathematical contexts and translates into a deeper appreciation for number theory's underlying principles. This article has provided a detailed exploration of factor pairs, specifically for the number 32, but the techniques and concepts presented can be applied to any positive integer, thereby broadening your mathematical understanding and problem-solving capabilities. The journey of exploring numbers and their relationships, as demonstrated by this exploration of factor pairs, unveils the elegant structure and intricate beauty inherent within the world of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is A Factor Pair Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
