What Is 9 To The Power Of 4
listenit
May 24, 2025 · 5 min read
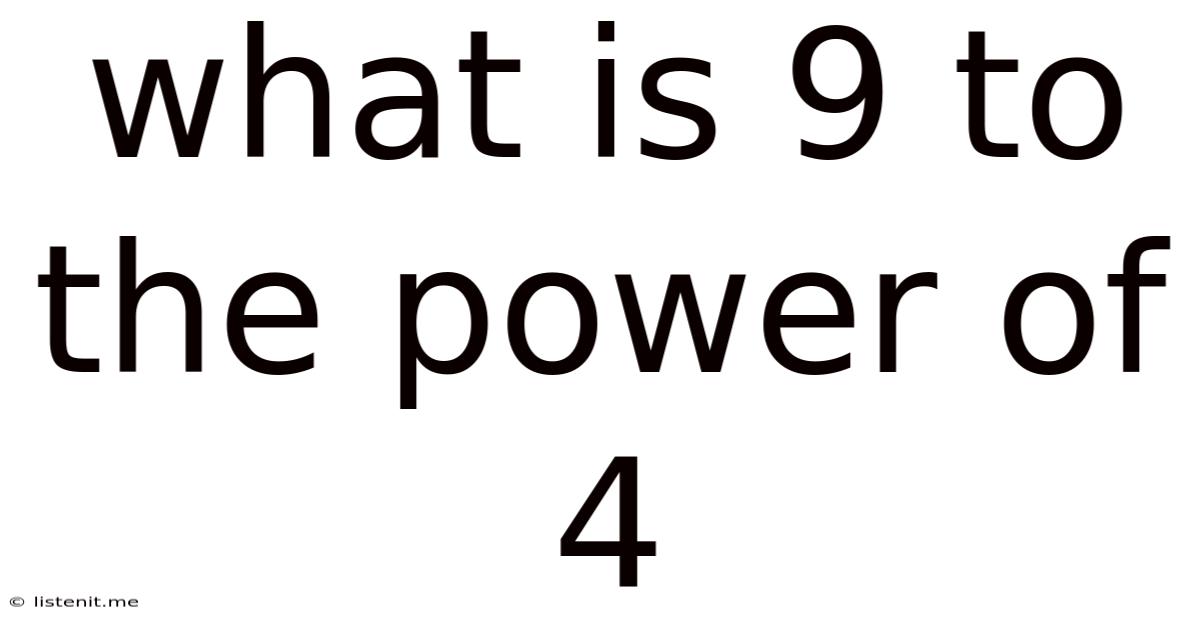
Table of Contents
What is 9 to the Power of 4? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 9 to the power of 4?" opens a door to a fascinating world of mathematics, specifically the realm of exponents. While the answer itself is straightforward (6561), understanding the concept behind it unlocks a wealth of knowledge applicable in various fields, from basic arithmetic to advanced calculus and even computer science. This article will not only provide the answer but will delve deep into the meaning of exponents, exploring their properties, practical applications, and related mathematical concepts.
Understanding Exponents: The Power of Repeated Multiplication
At its core, an exponent represents repeated multiplication. The expression 9<sup>4</sup> means 9 multiplied by itself four times: 9 * 9 * 9 * 9. The base number (9) is the number being multiplied, and the exponent (4) indicates how many times the base is multiplied by itself. This fundamental concept is crucial for understanding more complex mathematical operations.
Key Terminology: Base, Exponent, and Power
Let's clarify the terminology:
- Base: The number being multiplied repeatedly (in our case, 9).
- Exponent: The number indicating how many times the base is multiplied by itself (in our case, 4). Also known as the power or index.
- Power: The result of raising the base to the exponent (in our case, 6561). The entire expression, 9<sup>4</sup>, is often referred to as "9 raised to the power of 4" or "9 to the fourth power."
Calculating 9 to the Power of 4: Step-by-Step
Calculating 9<sup>4</sup> is a straightforward process:
- Start with the base: 9
- Multiply by the base: 9 * 9 = 81
- Multiply by the base again: 81 * 9 = 729
- Multiply by the base one last time: 729 * 9 = 6561
Therefore, 9 to the power of 4 is 6561.
Beyond the Calculation: Exploring the Properties of Exponents
The simplicity of calculating 9<sup>4</sup> shouldn't overshadow the rich mathematical properties associated with exponents. Understanding these properties is crucial for more advanced calculations and problem-solving.
Product of Powers
When multiplying two numbers with the same base, you can add their exponents: a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>. For instance, 9<sup>2</sup> * 9<sup>2</sup> = 9<sup>2+2</sup> = 9<sup>4</sup> = 6561.
Quotient of Powers
When dividing two numbers with the same base, you can subtract their exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. This property is equally important for simplifying expressions.
Power of a Power
When raising a power to another power, you multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>. For example, (9<sup>2</sup>)<sup>2</sup> = 9<sup>22</sup> = 9<sup>4</sup> = 6561.
Power of a Product
When raising a product to a power, you raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. This rule extends to more than two factors.
Power of a Quotient
Similarly, when raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. This rule requires b ≠ 0 to avoid division by zero.
Practical Applications of Exponents: From Science to Finance
The concept of exponents isn't confined to abstract mathematical exercises. It finds widespread application in numerous fields:
Science and Engineering
- Compound Interest: The growth of an investment with compound interest is calculated using exponents. The formula involves the principal amount, interest rate, and time period, all combined using exponential functions.
- Population Growth: Modeling population growth often utilizes exponential functions, reflecting the multiplicative nature of reproduction.
- Radioactive Decay: The decay of radioactive substances follows an exponential decay model, where the amount of remaining material decreases exponentially over time.
- Physics: Exponents are fundamental in various physics formulas, such as calculating the energy of a photon or describing the inverse square law of gravity.
- Computer Science: Exponential notation is crucial in representing large numbers and performing calculations efficiently in computer algorithms. Computational complexity is often expressed using exponential functions (e.g., exponential time complexity).
Finance and Economics
- Compound Interest (reiterated): As mentioned earlier, understanding compound interest is crucial in personal finance, investments, and loan calculations. The power of exponential growth is evident in the long-term accumulation of wealth.
- Inflation: Inflation's impact on purchasing power is often expressed exponentially, showing how prices rise over time.
- Economic Growth Models: Many economic growth models utilize exponential functions to predict future economic activity and resource allocation.
Everyday Life
While less obvious, exponents also play a subtle role in everyday life:
- Unit Conversions: Converting between units often involves raising numbers to powers (e.g., converting cubic meters to cubic centimeters).
- Area and Volume Calculations: Calculating the area of a square (side<sup>2</sup>) or the volume of a cube (side<sup>3</sup>) directly uses exponents.
Exploring Related Mathematical Concepts
Understanding exponents opens the door to a broader understanding of several interconnected mathematical concepts:
- Scientific Notation: Scientific notation uses exponents to represent very large or very small numbers concisely (e.g., 6.022 x 10<sup>23</sup>, Avogadro's number).
- Logarithms: Logarithms are the inverse operation of exponents. If a<sup>x</sup> = y, then log<sub>a</sub>y = x. Understanding logarithms is essential in solving exponential equations and analyzing logarithmic scales (e.g., the Richter scale for earthquakes).
- Exponential Functions: Exponential functions are functions of the form f(x) = a<sup>x</sup>, where 'a' is a constant. These functions are crucial in modeling growth and decay processes.
- Differential and Integral Calculus: Derivatives and integrals of exponential functions play a vital role in calculus, with applications spanning numerous scientific and engineering disciplines.
Conclusion: The Enduring Significance of Exponents
The seemingly simple calculation of 9<sup>4</sup> = 6561 serves as a gateway to a far-reaching and deeply significant mathematical concept. Exponents are far more than just a tool for repeated multiplication; they are fundamental building blocks in numerous mathematical operations and applications across various scientific, engineering, and financial domains. A thorough understanding of exponents and their properties is essential for anyone seeking a strong foundation in mathematics and its practical applications in the real world. From understanding compound interest to modeling population growth, the power of exponents is undeniable and their influence far-reaching.
Latest Posts
Latest Posts
-
How Do You Calculate Depreciation Of Equipment
May 24, 2025
-
February 9th Day Of The Week
May 24, 2025
-
2 3 Divided By 5 6
May 24, 2025
-
What Is 1 6 Divided By 4
May 24, 2025
-
What Is 5 4 Squared As A Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.