What Is 8 3/4 Expressed As A Fraction
listenit
May 24, 2025 · 5 min read
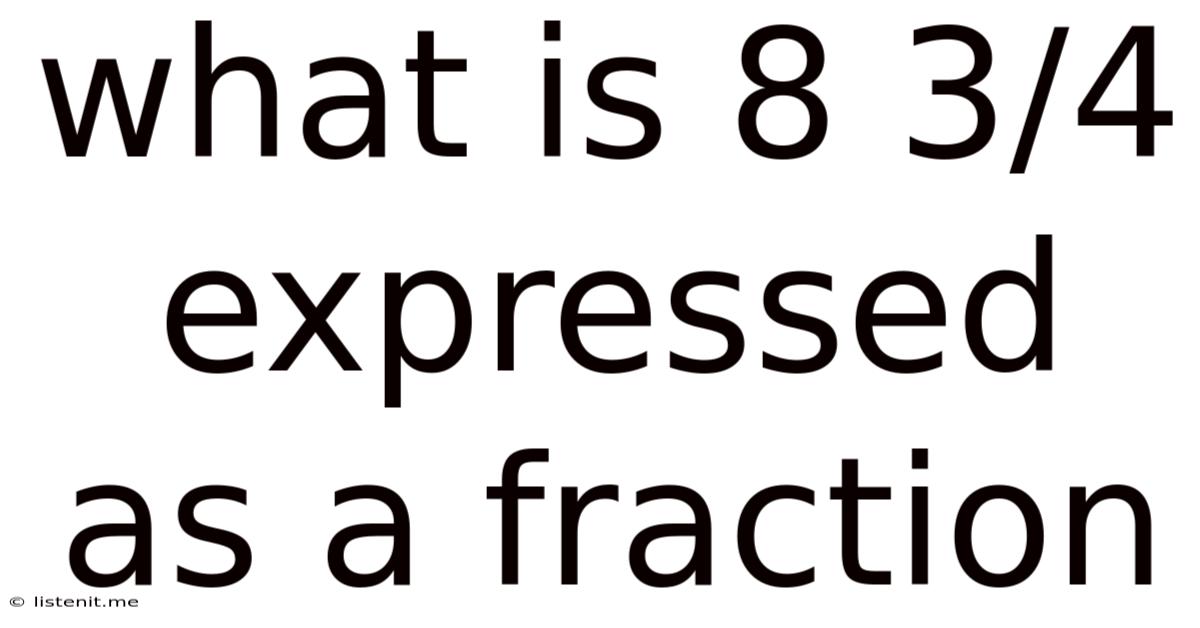
Table of Contents
What is 8 3/4 Expressed as a Fraction? A Deep Dive into Mixed Numbers and Improper Fractions
The question, "What is 8 3/4 expressed as a fraction?" might seem deceptively simple at first glance. However, it opens the door to a deeper understanding of fundamental mathematical concepts like mixed numbers, improper fractions, and the crucial process of converting between them. This comprehensive guide will not only answer the question directly but also explore the underlying principles, providing you with a solid foundation in fractional arithmetic.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the conversion, let's define our key terms:
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). Our example, 8 3/4, is a mixed number: 8 is the whole number, and 3/4 is the proper fraction.
Improper Fraction: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Improper fractions represent values greater than or equal to one. The goal of our conversion is to express 8 3/4 as an improper fraction.
Converting a Mixed Number to an Improper Fraction: The Step-by-Step Process
The conversion process is straightforward and involves two main steps:
Step 1: Multiply the whole number by the denominator.
In our example, 8 3/4, the whole number is 8, and the denominator is 4. Multiplying these together gives us 8 * 4 = 32.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 3. Adding this to the result from Step 1 (32), we get 32 + 3 = 35.
Step 3: Keep the same denominator.
The denominator remains unchanged throughout the conversion process. Therefore, the denominator stays as 4.
Step 4: Combine the results to form the improper fraction.
Combining the result from Step 2 (35) as the numerator and keeping the denominator as 4, we arrive at our improper fraction: 35/4.
Therefore, 8 3/4 expressed as a fraction is 35/4.
Visualizing the Conversion: A Practical Approach
Understanding the concept visually can often solidify mathematical comprehension. Imagine you have eight whole pizzas and three-quarters of another pizza. To express this as a single fraction, we need to convert all the pizzas into quarters.
Each whole pizza can be divided into four quarters. Since we have eight whole pizzas, that's 8 * 4 = 32 quarters. Adding the three quarters from the remaining pizza, we get a total of 32 + 3 = 35 quarters. This is represented as 35/4.
Why is this Conversion Important?
Converting between mixed numbers and improper fractions is a crucial skill in various mathematical contexts, including:
- Simplification: Improper fractions, while appearing more complex, sometimes simplify more easily than mixed numbers.
- Calculations: Performing calculations (addition, subtraction, multiplication, and division) with improper fractions is often simpler and more consistent than working with mixed numbers.
- Advanced Mathematics: The concept is foundational for more advanced mathematical concepts, including algebra and calculus.
Exploring Other Examples: Reinforcing the Concept
Let's reinforce our understanding with a few more examples:
Example 1: Converting 5 2/3 to an improper fraction.
- Multiply the whole number by the denominator: 5 * 3 = 15
- Add the numerator: 15 + 2 = 17
- Keep the same denominator: 3
- Improper fraction: 17/3
Example 2: Converting 2 1/8 to an improper fraction.
- Multiply the whole number by the denominator: 2 * 8 = 16
- Add the numerator: 16 + 1 = 17
- Keep the same denominator: 8
- Improper fraction: 17/8
Example 3: Converting 10 5/6 to an improper fraction.
- Multiply the whole number by the denominator: 10 * 6 = 60
- Add the numerator: 60 + 5 = 65
- Keep the same denominator: 6
- Improper fraction: 65/6
The Reverse Process: Converting Improper Fractions to Mixed Numbers
It's equally important to understand the reverse process – converting an improper fraction to a mixed number. This involves dividing the numerator by the denominator:
Example: Converting 35/4 to a mixed number.
- Divide the numerator by the denominator: 35 ÷ 4 = 8 with a remainder of 3.
- The quotient becomes the whole number: 8
- The remainder becomes the numerator: 3
- The denominator remains the same: 4
- Mixed number: 8 3/4
Practical Applications of Mixed Numbers and Improper Fractions
Mixed numbers and improper fractions appear frequently in everyday life and various professional fields:
- Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities.
- Construction and Engineering: Precise measurements frequently involve fractions.
- Finance: Calculating interest and proportions often necessitates the use of fractions.
- Data Analysis: Representing data and proportions often uses fractional representations.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Understanding the conversion between mixed numbers and improper fractions is fundamental to mastering fractional arithmetic. This seemingly simple conversion unlocks a deeper understanding of numbers and their representation, which is crucial for success in various mathematical endeavors. By practicing these conversions and understanding the underlying principles, you'll build a strong foundation for more advanced mathematical concepts and problem-solving. Remember, consistent practice is key to solidifying your understanding and building confidence in working with fractions. The ability to easily switch between mixed numbers and improper fractions will empower you to tackle more complex mathematical challenges with ease and precision.
Latest Posts
Latest Posts
-
20 Out Of 60 Is What Percent
May 25, 2025
-
0 1 Of What Number Is 4
May 25, 2025
-
Whats The Date 28 Days From Now
May 25, 2025
-
How Many Years Is 1987 To 2024
May 25, 2025
-
300 000 Loan For 10 Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 3/4 Expressed As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.