What Is 8/12 - 4/8 Reduced To The Lowest Terms
listenit
May 25, 2025 · 5 min read
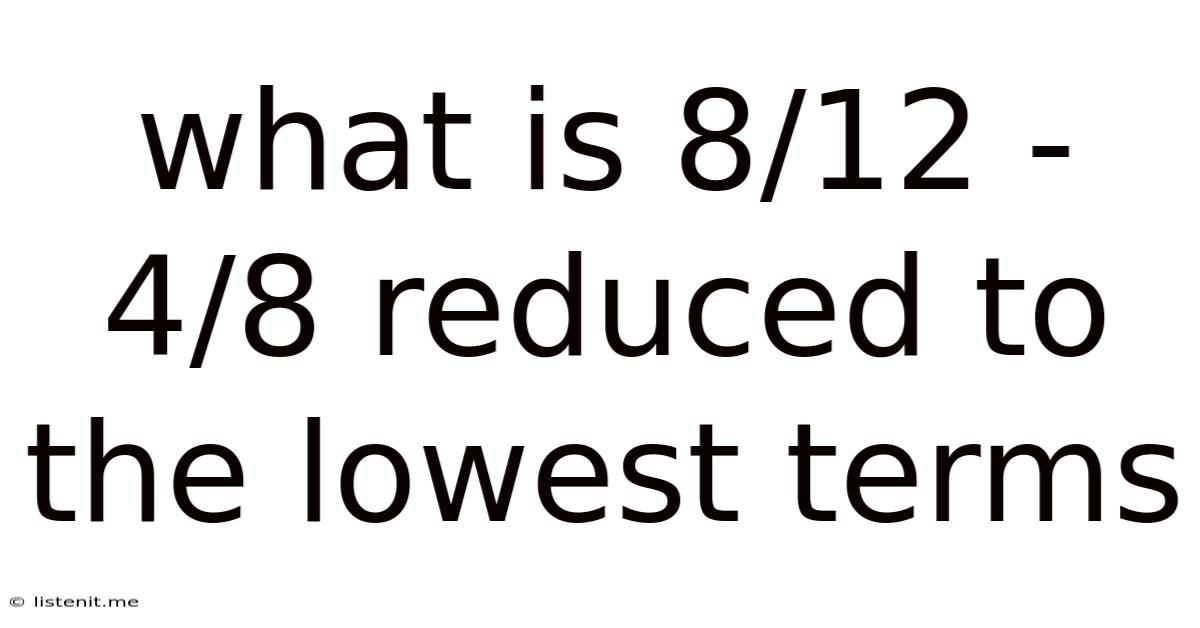
Table of Contents
What is 8/12 - 4/8 Reduced to the Lowest Terms? A Comprehensive Guide to Fraction Subtraction and Simplification
Understanding fractions and how to manipulate them is a fundamental skill in mathematics. This guide will walk you through the process of subtracting fractions, specifically focusing on the problem 8/12 - 4/8, and then simplifying the result to its lowest terms. We'll cover the core concepts, step-by-step calculations, and explore the broader applications of fraction simplification.
Understanding Fractions: Numerator and Denominator
Before diving into the subtraction, let's review the basics of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) indicates you have three parts, and the denominator (4) indicates the whole is divided into four equal parts.
Finding a Common Denominator
Subtracting (or adding) fractions requires them to have the same denominator. This common denominator represents the same size "pieces" we are working with, ensuring accurate comparison and calculation. If the fractions don't share a common denominator, we must find one before proceeding.
Let's look at our fractions: 8/12 and 4/8. Their denominators, 12 and 8, are different. To find the least common denominator (LCD), we need to find the smallest number that both 12 and 8 divide into evenly. One way to do this is to list the multiples of each number:
- Multiples of 12: 12, 24, 36, 48, 60...
- Multiples of 8: 8, 16, 24, 32, 40...
The smallest number appearing in both lists is 24. Therefore, 24 is the least common denominator (LCD) for 8/12 and 4/8.
Converting Fractions to Equivalent Fractions
Now that we have our LCD (24), we need to convert both fractions to equivalent fractions with a denominator of 24. To do this, we multiply both the numerator and the denominator of each fraction by the same number that will result in a denominator of 24.
For 8/12:
To get a denominator of 24, we need to multiply 12 by 2 (12 x 2 = 24). Therefore, we must also multiply the numerator (8) by 2:
8/12 = (8 x 2) / (12 x 2) = 16/24
For 4/8:
To get a denominator of 24, we need to multiply 8 by 3 (8 x 3 = 24). Therefore, we must also multiply the numerator (4) by 3:
4/8 = (4 x 3) / (8 x 3) = 12/24
Subtracting the Fractions
Now that both fractions have the same denominator, we can subtract them:
16/24 - 12/24 = (16 - 12) / 24 = 4/24
Reducing to Lowest Terms (Simplifying the Fraction)
The fraction 4/24 is not in its simplest form. To simplify a fraction to its lowest terms, we need to find the greatest common divisor (GCD) of the numerator (4) and the denominator (24). The GCD is the largest number that divides both the numerator and denominator evenly.
The factors of 4 are 1, 2, and 4. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
The greatest common factor of 4 and 24 is 4.
To simplify, we divide both the numerator and the denominator by the GCD (4):
4/24 = (4 ÷ 4) / (24 ÷ 4) = 1/6
Therefore, 8/12 - 4/8 reduced to its lowest terms is 1/6.
Alternative Method: Simplifying Before Subtraction
While the above method is perfectly valid, we can sometimes simplify the fractions before finding a common denominator. This can make the calculations easier.
Let's revisit the original fractions: 8/12 and 4/8.
Simplifying 8/12:
The GCD of 8 and 12 is 4. Simplifying 8/12:
8/12 = (8 ÷ 4) / (12 ÷ 4) = 2/3
Simplifying 4/8:
The GCD of 4 and 8 is 4. Simplifying 4/8:
4/8 = (4 ÷ 4) / (8 ÷ 4) = 1/2
Now we have 2/3 - 1/2. The LCD of 3 and 2 is 6.
Converting to equivalent fractions:
2/3 = (2 x 2) / (3 x 2) = 4/6 1/2 = (1 x 3) / (2 x 3) = 3/6
Subtracting:
4/6 - 3/6 = (4 - 3) / 6 = 1/6
As you can see, we arrive at the same answer: 1/6.
Real-World Applications of Fraction Subtraction and Simplification
Understanding fraction subtraction and simplification is crucial in various real-world scenarios:
- Cooking and Baking: Following recipes often involves precise measurements, requiring accurate fraction calculations.
- Construction and Engineering: Precise measurements are vital in construction projects, ensuring everything fits perfectly.
- Finance: Calculating budgets, understanding interest rates, and managing finances often require fraction manipulation.
- Sewing and Tailoring: Accurate measurements and adjustments are necessary for creating well-fitting garments.
- Data Analysis: Representing and interpreting data often involves using fractions and percentages.
Beyond the Basics: More Complex Fraction Problems
The principles discussed here – finding a common denominator, subtracting fractions, and simplifying to lowest terms – are fundamental to solving more complex fraction problems. These include:
- Adding and Subtracting more than two fractions: The same principles apply; find the LCD and then perform the addition or subtraction.
- Mixed numbers: Mixed numbers (like 1 1/2) combine whole numbers and fractions. Convert them to improper fractions before performing calculations.
- Multiplying and dividing fractions: Different rules apply to these operations; you don't need a common denominator.
Mastering these fundamental skills will provide a solid foundation for tackling more advanced mathematical concepts. Practice is key! Try solving similar problems, gradually increasing the complexity to solidify your understanding.
Key Takeaways
This guide has thoroughly explained how to solve 8/12 - 4/8, emphasizing the importance of finding a common denominator, performing the subtraction, and simplifying the result to its lowest terms (1/6). We've explored alternative methods and highlighted the real-world relevance of these fundamental fraction operations. Remember, a strong understanding of fractions is a building block for success in mathematics and numerous real-world applications. Continuous practice and exploration of more complex problems will enhance your proficiency and confidence in handling fractions.
Latest Posts
Latest Posts
-
How To Calculate Interest On A Car
May 25, 2025
-
What Is The Lowest Common Multiple Of 18 And 15
May 25, 2025
-
26 Years Old What Year Born
May 25, 2025
-
What Is The Greatest Common Factor Of 40 And 32
May 25, 2025
-
Semester Grade Calculator Without Final Exam
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/12 - 4/8 Reduced To The Lowest Terms . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.