What Is 6 Divided By 1 5
listenit
May 24, 2025 · 4 min read
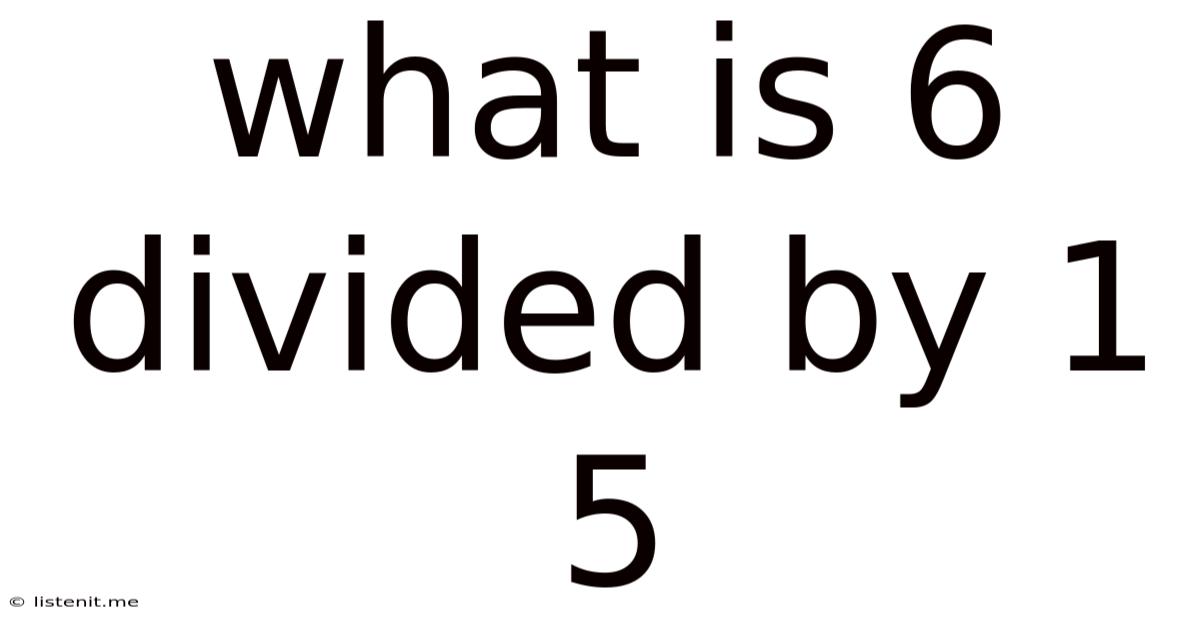
Table of Contents
What is 6 Divided by 1/5? Understanding Fraction Division
The question "What is 6 divided by 1/5?" might seem simple at first glance, but it touches upon a crucial concept in mathematics: division involving fractions. Many people struggle with fraction division, but with a clear understanding of the underlying principles, it becomes straightforward. This comprehensive guide will not only answer the question but also delve into the why behind the solution, exploring different approaches and clarifying common misconceptions.
Deconstructing the Problem: 6 ÷ 1/5
Before diving into the solution, let's break down the problem: 6 ÷ 1/5. This means we're asking: "How many times does 1/5 go into 6?"
This isn't immediately intuitive like dividing whole numbers. We're not simply splitting 6 into 5 equal parts. Instead, we're figuring out how many 1/5 portions exist within 6 whole units.
Method 1: The "Keep, Change, Flip" Method
This is the most popular and arguably the easiest method for dividing fractions. It's often remembered by the mnemonic "Keep, Change, Flip":
- Keep the first number (the dividend) as it is: 6.
- Change the division sign (÷) to a multiplication sign (×).
- Flip the second number (the divisor) – also known as finding its reciprocal. The reciprocal of 1/5 is 5/1, or simply 5.
Therefore, 6 ÷ 1/5 becomes 6 × 5.
This simplifies to: 6 × 5 = 30
Therefore, 6 divided by 1/5 is 30.
Method 2: Visual Representation
Imagine you have 6 pizzas. Each pizza is cut into 5 equal slices (1/5 of a pizza). How many slices do you have in total?
You would have 6 pizzas * 5 slices/pizza = 30 slices.
This visual approach helps to solidify the understanding of why the "Keep, Change, Flip" method works. It demonstrates the concept of how many smaller fractions are contained within a whole number.
Method 3: Using Common Denominators
This method is less common for this specific problem but showcases a more fundamental approach to fraction division. It relies on converting the whole number into a fraction and then applying the rule for dividing fractions with common denominators.
- Convert the whole number to a fraction: 6 can be written as 6/1.
- Find a common denominator: The common denominator of 6/1 and 1/5 is 5.
- Convert fractions to have the common denominator: 6/1 becomes 30/5 (multiplying the numerator and denominator by 5).
- Divide the numerators: (30/5) ÷ (1/5) = 30 ÷ 1 = 30.
This method reinforces the concept of equivalent fractions and demonstrates the underlying principles of fraction division more explicitly.
Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" method is a shortcut based on the fundamental rule of fraction division:
a ÷ b/c = a × c/b
Where 'a' is the dividend, 'b' is the numerator of the divisor, and 'c' is the denominator of the divisor. The method simply streamlines this rule. Multiplying by the reciprocal is equivalent to dividing by the original fraction.
Addressing Common Misconceptions
Many people mistakenly try to divide 6 by 1 and then divide by 5, arriving at the incorrect answer of 6/5 or 1.2. This shows a fundamental misunderstanding of fraction division. It is crucial to remember that dividing by a fraction is not the same as dividing by each part of the fraction independently.
Another common error is forgetting to flip the fraction before multiplying. This leads to incorrect calculations and results.
Expanding the Concept: Real-World Applications
Understanding fraction division extends far beyond simple mathematical exercises. It finds applications in various real-world scenarios:
- Cooking: Scaling recipes up or down involves dividing or multiplying fractional ingredients.
- Construction: Calculating material quantities often requires dividing lengths or areas by fractions.
- Sewing: Pattern adjustments and fabric calculations involve fraction division.
- Finance: Calculating proportions of investments or portions of budgets requires fractional arithmetic.
Mastering fraction division is crucial for handling these real-world situations accurately and efficiently.
Practice Problems to Reinforce Understanding
To solidify your understanding, try these practice problems:
- 8 ÷ 1/2
- 10 ÷ 2/5
- 12 ÷ 3/4
- 15 ÷ 1/3
- 20 ÷ 5/8
Remember to use the methods outlined above and check your answers.
Conclusion: Mastering Fraction Division
Understanding how to divide by a fraction is a fundamental skill in mathematics with wide-ranging applications. By mastering the "Keep, Change, Flip" method, visualizing the problem, or using the common denominator approach, you can confidently tackle any fraction division problem. Regular practice and understanding the underlying principles will eliminate confusion and build a strong foundation in mathematics. Remember, practice makes perfect! Consistent effort and a willingness to understand the "why" behind the mathematical operations will lead to success.
Latest Posts
Latest Posts
-
What Is 2 Divided By 7
May 24, 2025
-
15 Months Is How Many Days
May 24, 2025
-
Greatest Common Factor For 12 And 16
May 24, 2025
-
28 Days From October 30 2024
May 24, 2025
-
What Time Is An Hour And A Half From Now
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.