What Is 50 Percent Of 12
listenit
May 12, 2025 · 5 min read
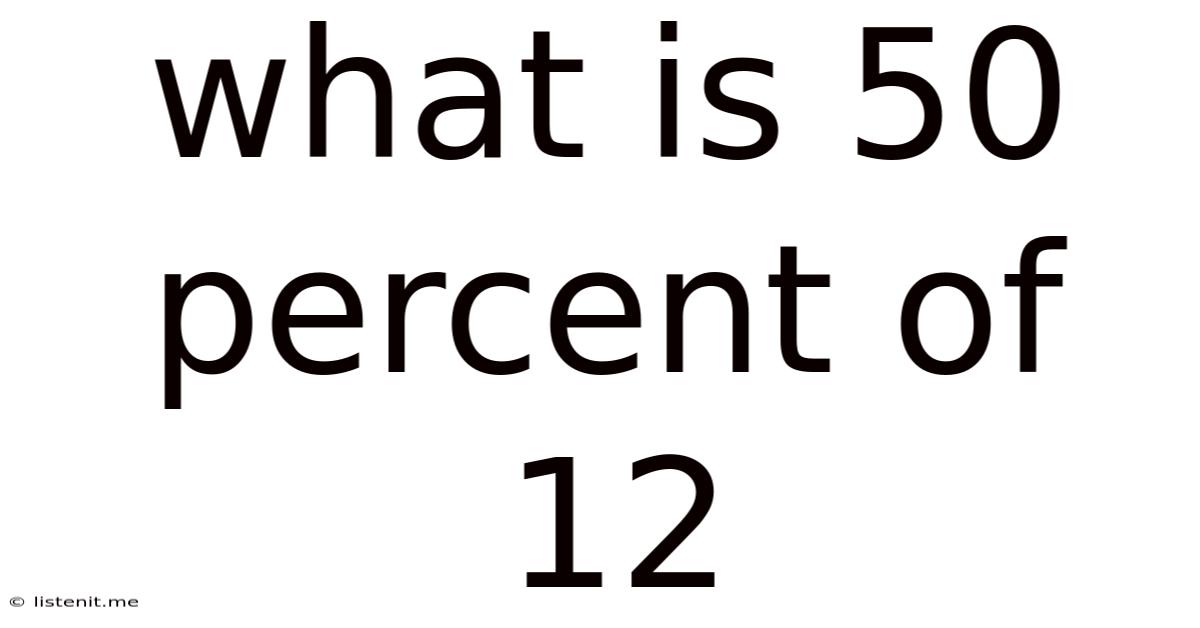
Table of Contents
What is 50 Percent of 12? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 50 percent of 12?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (6), understanding the underlying principles of percentages and their diverse uses is crucial in various fields, from everyday budgeting to advanced financial modeling. This comprehensive guide will not only answer the initial question but delve into the intricacies of percentage calculations, explore different methods for solving such problems, and showcase real-world examples where this fundamental concept plays a vital role.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50 percent means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Understanding this fundamental concept is key to solving any percentage-related problem.
Calculating 50 Percent of 12: Three Approaches
There are several ways to calculate 50 percent of 12. Let's explore three common methods:
1. The Fraction Method:
Since 50 percent is equivalent to the fraction 1/2, calculating 50 percent of 12 is the same as finding half of 12. This is a simple division:
12 ÷ 2 = 6
Therefore, 50 percent of 12 is 6.
2. The Decimal Method:
Converting the percentage to a decimal simplifies the calculation. 50 percent is equal to 0.5. Multiplying this decimal by 12 gives us the answer:
12 x 0.5 = 6
Again, 50 percent of 12 is 6.
3. The Proportion Method:
This method uses proportions to solve the problem. We can set up a proportion:
50/100 = x/12
where 'x' represents 50 percent of 12. To solve for x, we cross-multiply:
50 x 12 = 100 x 600 = 100x x = 600/100 x = 6
This confirms that 50 percent of 12 is 6.
Beyond the Basics: Expanding Percentage Calculations
While calculating 50 percent of 12 is relatively straightforward, the principles involved can be applied to more complex percentage problems. Understanding these principles is vital for various applications.
Calculating Other Percentages:
The same methods can be used to calculate any percentage of any number. For instance, to find 25 percent of 12:
- Fraction method: 25 percent is 1/4, so 12 ÷ 4 = 3
- Decimal method: 25 percent is 0.25, so 12 x 0.25 = 3
- Proportion method: 25/100 = x/12; x = 3
Finding the Original Value:
Conversely, if you know the percentage and the resulting value, you can calculate the original value. For example, if 50 percent of a number is 6, what is the original number?
This can be solved using a simple equation:
0.5x = 6 x = 6/0.5 x = 12
Percentage Increase and Decrease:
Percentages are often used to represent increases or decreases in values. For instance, if a price increases by 10 percent, you calculate the increase and add it to the original price. If a price decreases by 20 percent, you calculate the decrease and subtract it from the original price.
Compound Interest:
In finance, compound interest calculations rely heavily on percentages. Compound interest is interest earned not only on the principal amount but also on accumulated interest from previous periods. The formula involves repeated percentage calculations.
Real-world Applications of Percentages:
Percentages are ubiquitous in daily life:
- Sales and Discounts: Stores frequently advertise discounts as percentages (e.g., "20% off").
- Taxes: Sales tax, income tax, and other taxes are expressed as percentages.
- Interest Rates: Interest rates on loans and savings accounts are expressed as percentages.
- Statistical Data: Percentages are used extensively in data analysis and reporting to represent proportions and trends.
- Financial Statements: Financial statements such as balance sheets and income statements use percentages to analyze financial performance.
- Science and Engineering: Percentages are used to express concentrations, efficiencies, and other measurements.
Advanced Percentage Problems and Solutions
Let's explore a few more complex percentage problems to further solidify our understanding:
Problem 1: A shirt originally priced at $25 is on sale for 30% off. What is the sale price?
Solution:
- Calculate the discount: 25 x 0.30 = $7.50
- Subtract the discount from the original price: 25 - 7.50 = $17.50 The sale price is $17.50.
Problem 2: A store owner increases the price of an item by 15% to $34.50. What was the original price?
Solution:
Let x be the original price. Then:
x + 0.15x = 34.50 1.15x = 34.50 x = 34.50 / 1.15 x = 30
The original price was $30.
Problem 3: A student scored 80 out of 100 on a test. What is their percentage score?
Solution:
(80/100) x 100 = 80%
The student's percentage score is 80%.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill applicable across various disciplines. While seemingly simple, the ability to accurately calculate and interpret percentages is essential for personal finance, business decisions, data analysis, and much more. From calculating simple discounts to understanding complex financial models, a firm grasp of percentage calculations empowers individuals to make informed choices and navigate the quantitative aspects of daily life effectively. The seemingly basic question "What is 50 percent of 12?" ultimately serves as a springboard to a deeper understanding of a crucial mathematical concept with far-reaching implications. By mastering these principles, you're equipping yourself with a valuable tool for success in many aspects of life.
Latest Posts
Latest Posts
-
The Density Of Silver Is 10 5 G Cm3
May 12, 2025
-
How Many Atoms Are In Nh3
May 12, 2025
-
Why Is Displacement A Vector Quantity
May 12, 2025
-
Is Nh4oh An Acid Or Base
May 12, 2025
-
Limits At Infinity With Trig Functions
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.