What Is 5 Percent Of 250
listenit
May 24, 2025 · 5 min read
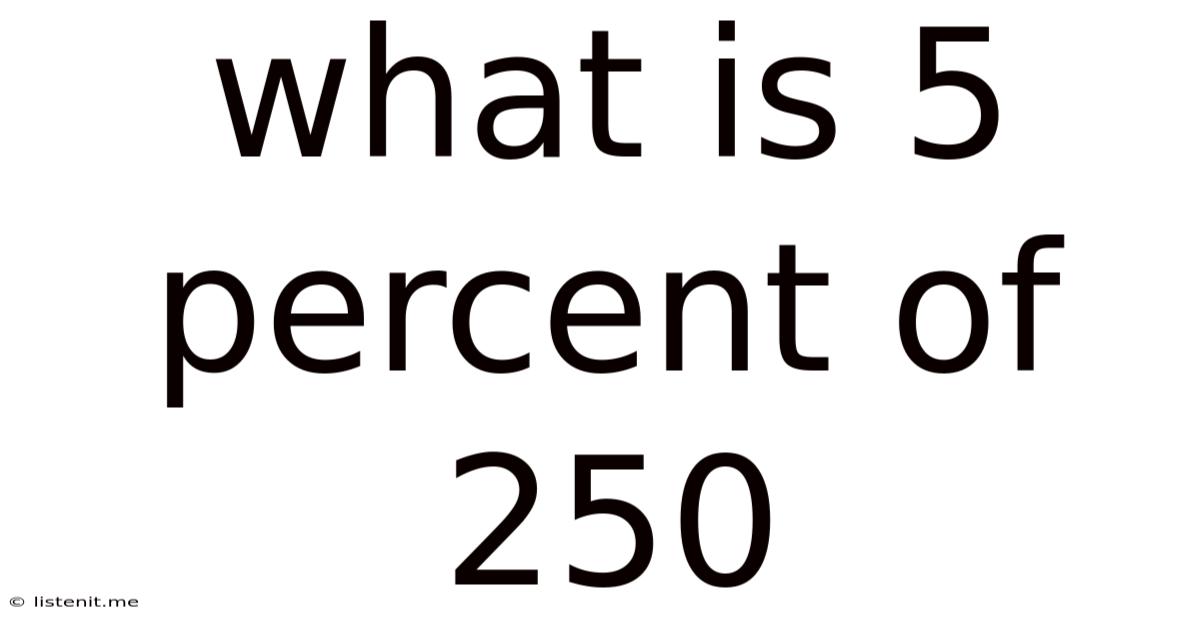
Table of Contents
What is 5 Percent of 250? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across various fields, from everyday finances to complex scientific analyses. This article will not only answer the question, "What is 5 percent of 250?" but will also delve into the underlying concepts, providing a comprehensive understanding of percentages and their practical uses.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 5 percent means 5 out of every 100. We represent this as 5/100 or 0.05 in decimal form. This seemingly simple concept forms the basis for numerous calculations in various domains.
Key Concepts:
- Percentage: The portion of a whole represented as a number out of 100.
- Decimal: The equivalent representation of a percentage as a fraction with a denominator of 100 (e.g., 5% = 0.05).
- Fraction: The representation of a percentage as a fraction (e.g., 5% = 5/100).
Calculating 5 Percent of 250
Now, let's address the core question: What is 5 percent of 250? There are several methods to solve this problem:
Method 1: Using the Decimal Form
- Convert the percentage to a decimal: 5% = 0.05
- Multiply the decimal by the number: 0.05 x 250 = 12.5
Therefore, 5 percent of 250 is 12.5.
Method 2: Using the Fraction Form
- Convert the percentage to a fraction: 5% = 5/100
- Multiply the fraction by the number: (5/100) x 250 = 1250/100
- Simplify the fraction: 1250/100 = 12.5
Again, we arrive at the answer: 5 percent of 250 is 12.5.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between the percentage, the whole, and the part.
We can set up a proportion:
5/100 = x/250
Where 'x' represents the unknown value (5 percent of 250). To solve for x, we cross-multiply:
100x = 5 x 250
100x = 1250
x = 1250/100
x = 12.5
Thus, 5 percent of 250 is 12.5.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating interest: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding these calculations is essential for managing personal finances effectively.
- Discounts and Sales Tax: Percentages are used extensively in calculating discounts offered during sales and sales taxes added to purchases. Knowing how to calculate these accurately can save you money and avoid errors.
- Investment Returns: Investors use percentage calculations to track the returns on their investments, assessing the growth or decline of their portfolios.
- Calculating Tips: Determining the appropriate tip amount in restaurants often involves calculating a percentage of the total bill.
2. Science and Research:
- Statistical Analysis: Percentages are fundamental in statistical analysis, representing proportions within datasets and contributing to interpreting results.
- Data Representation: Presenting data using percentages allows for easy comparison and interpretation across different samples or groups.
- Scientific Experiments: Percentages are frequently used to express the yield or success rate of scientific experiments.
3. Everyday Life:
- Cooking and Baking: Recipes often use percentages to indicate the proportions of ingredients. Understanding these percentages is crucial for accurate cooking and baking.
- Shopping and Comparing Prices: Comparing prices of products and identifying discounts or deals often requires understanding and calculating percentages.
- Grading Systems: Many educational systems use percentages to represent grades and scores on assessments.
Beyond the Basics: Advanced Percentage Calculations
While the calculation of 5 percent of 250 is relatively straightforward, other percentage problems require more complex approaches. Here are some examples:
1. Finding the Percentage Increase or Decrease:
Calculating the percentage change between two values involves determining the difference between the values, dividing by the original value, and then multiplying by 100. For example, finding the percentage increase from 200 to 250:
(250 - 200) / 200 x 100 = 25%
2. Finding the Original Value:
If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 10% of a number is 25, then the original number is 250 (25 / 0.10 = 250).
3. Calculating Compound Percentages:
Compounding involves applying a percentage to a value repeatedly over time. This is particularly important in scenarios involving interest or investment growth. For example, calculating the value of an investment after several years with a fixed annual interest rate.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The best way to master percentage calculations is to practice regularly. Solve various problems, starting with simple ones and gradually increasing the complexity.
- Use Online Calculators: While understanding the underlying principles is important, online calculators can be a useful tool for checking your work or quickly solving complex problems.
- Understand the Concepts: Focus on understanding the core concepts of percentages, decimals, and fractions. This solid foundation will help you tackle more advanced problems.
- Break Down Complex Problems: When faced with complex problems, break them down into smaller, manageable steps. This will make the process easier and less daunting.
Conclusion: The Power of Percentage Calculations
The seemingly simple calculation of 5 percent of 250 opens the door to a world of practical applications. From managing personal finances to analyzing scientific data, understanding and mastering percentage calculations is a valuable skill for navigating various aspects of life. By understanding the underlying principles and practicing regularly, you can confidently tackle percentage-related problems and leverage this fundamental concept to its full potential. Remember, mastering percentage calculations isn't just about getting the right answer; it’s about understanding the underlying relationships and applying that knowledge to solve real-world problems effectively.
Latest Posts
Latest Posts
-
How Long Is 7am To 7pm
May 24, 2025
-
If You Are 28 What Year Were You Born
May 24, 2025
-
Greatest Common Factor Of 12 And 8
May 24, 2025
-
Whats The Date 14 Days From Today
May 24, 2025
-
8 Of 12 Is What Percent
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.