What Is 4 To The 2 Power
listenit
Mar 25, 2025 · 4 min read
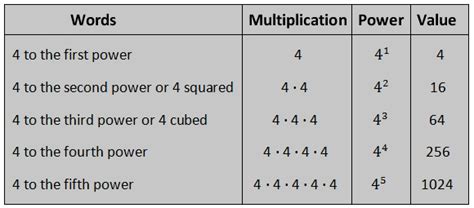
Table of Contents
What is 4 to the 2nd Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics, forming the bedrock for numerous advanced concepts. This comprehensive guide explores the seemingly simple question: "What is 4 to the 2nd power?" We'll delve into the meaning of exponents, explore various methods for calculating them, and uncover their practical applications across diverse fields.
Understanding Exponents: The Power of Repeated Multiplication
Before tackling 4 to the 2nd power, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's represented as a small superscript number placed to the right of the base.
For example, in the expression 4², the number 4 is the base, and the number 2 is the exponent. This expression signifies 4 multiplied by itself 2 times: 4 x 4 = 16.
Therefore, 4 to the 2nd power is 16.
Calculating 4 to the 2nd Power: Different Approaches
While the calculation of 4² is straightforward, understanding different calculation methods is crucial for tackling more complex exponential problems.
Direct Multiplication: The Simplest Method
The most fundamental approach is direct multiplication. Simply multiply the base number (4) by itself the number of times indicated by the exponent (2):
4² = 4 x 4 = 16
Using a Calculator: Efficiency for Larger Numbers
For larger exponents or more complex calculations, a calculator provides a quick and efficient solution. Most calculators have an exponent function (often denoted as ^ or xʸ). Simply input the base (4), the exponent (2), and the calculator will instantly provide the result: 16.
Expanding the Concept: Exponents Beyond 2
While this article focuses on 4², let's briefly explore exponents beyond the second power to gain a broader perspective.
4 to the 3rd Power (4³)
4³ signifies 4 multiplied by itself three times: 4 x 4 x 4 = 64
4 to the Power of 0 (4⁰)
Any non-zero number raised to the power of 0 equals 1. Therefore, 4⁰ = 1.
4 to the Power of 1 (4¹)
Any number raised to the power of 1 equals itself. Therefore, 4¹ = 4.
4 to the Negative Power (4⁻²)
A negative exponent indicates the reciprocal of the positive exponent. Therefore, 4⁻² = 1/4² = 1/16 = 0.0625
Practical Applications of Exponents: Real-World Scenarios
Exponents are far from abstract mathematical concepts; they have practical applications across numerous fields:
Finance: Compound Interest Calculations
Compound interest, a cornerstone of financial planning, utilizes exponents to calculate the future value of an investment. The formula considers the principal amount, interest rate, and time period, with the exponent representing the number of compounding periods. Understanding exponents is crucial for effectively managing investments and loans.
Science: Exponential Growth and Decay
Many natural phenomena exhibit exponential growth or decay. For instance, population growth, radioactive decay, and the spread of diseases often follow exponential patterns. Exponents are vital tools for modeling and predicting these processes.
Computer Science: Binary Numbers and Data Storage
Computers operate using binary code (base-2). Exponents are essential for understanding how binary numbers represent data and how much storage space is required. For instance, 2¹⁰ (1024) represents the number of bytes in a kilobyte.
Engineering: Calculating Areas and Volumes
Exponents are fundamental in geometry and engineering for calculating areas and volumes of various shapes. For instance, the volume of a cube is side³, which directly employs exponents. Understanding exponents is critical for designing structures, machines, and systems.
Beyond the Basics: Advanced Exponential Concepts
While we've covered the basics of 4², understanding more advanced concepts further enriches your mathematical toolkit:
Scientific Notation: Expressing Very Large or Small Numbers
Scientific notation uses exponents to express extremely large or small numbers in a compact and manageable form. For instance, the speed of light (approximately 300,000,000 meters per second) can be written as 3 x 10⁸ m/s.
Logarithms: The Inverse of Exponents
Logarithms are the inverse of exponents. They allow you to determine the exponent required to obtain a specific value from a given base. Logarithms find applications in various fields, including chemistry, physics, and signal processing.
Exponential Functions: Modeling Growth and Decay
Exponential functions describe processes exhibiting exponential growth or decay. These functions are crucial for modeling various phenomena in science, engineering, and finance.
Fractional Exponents: Roots and Radicals
Fractional exponents represent roots and radicals. For instance, 4^(1/2) is equivalent to the square root of 4, which is 2. Understanding fractional exponents opens up possibilities for solving more complex equations.
Conclusion: The Power of Understanding Exponents
While the answer to "What is 4 to the 2nd power?" is simply 16, the underlying concepts of exponents have far-reaching implications. From basic arithmetic to complex scientific modeling, exponents are an essential mathematical tool. By grasping the fundamental principles and exploring their applications, you build a solid foundation for tackling more advanced mathematical concepts and problem-solving in diverse fields. The seemingly simple calculation of 4² serves as a gateway to a deeper understanding of the power and versatility of exponents. Continue exploring, and you’ll unlock even more of mathematics' fascinating capabilities.
Latest Posts
Latest Posts
-
3x 2y 2 In Slope Intercept Form
Mar 27, 2025
-
What Is 7 Over 25 As A Decimal
Mar 27, 2025
-
What Are The Common Factors Of 30 And 75
Mar 27, 2025
-
What Unit Is Work Measured In
Mar 27, 2025
-
Is Boron A Gas Liquid Or Solid
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
