What Is 4 Percent Of 200
listenit
May 25, 2025 · 6 min read
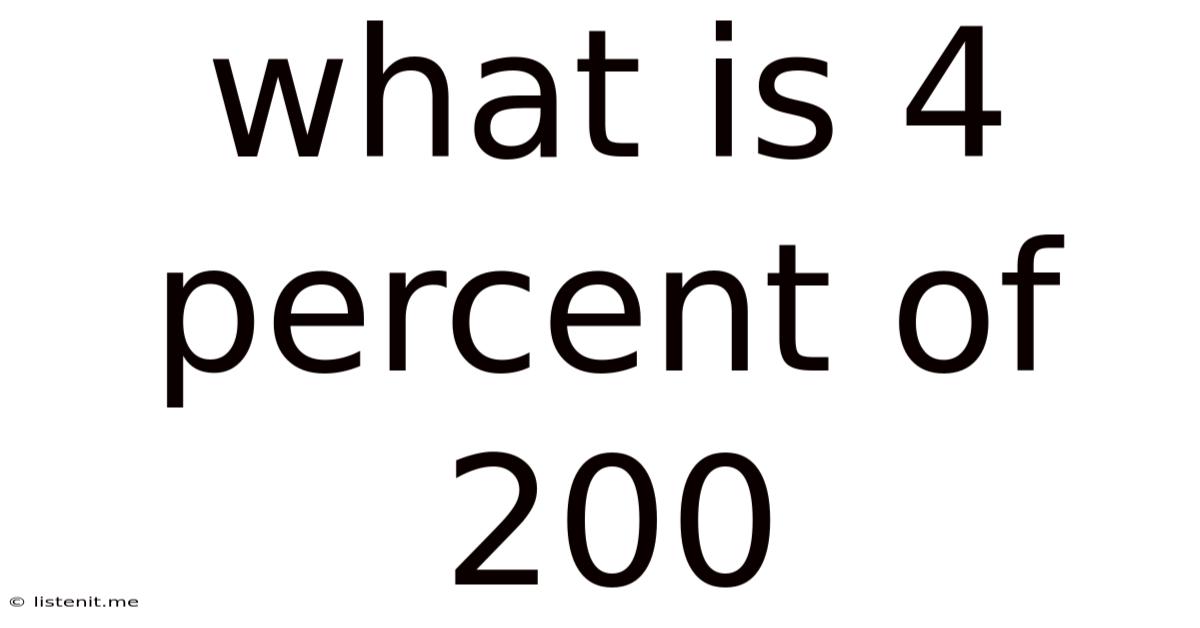
Table of Contents
What is 4 Percent of 200? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from finance and budgeting to sales, discounts, and even understanding statistical data. This article will thoroughly explore the question, "What is 4 percent of 200?", providing not only the answer but also a comprehensive understanding of the underlying concepts and practical applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol used to represent percentage is "%". Essentially, it represents a portion or proportion of a whole. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are invaluable tools because they allow us to:
- Compare proportions: Easily compare different quantities expressed as percentages, regardless of the original sizes. For example, comparing a 10% increase in sales across different stores is straightforward.
- Simplify complex data: Representing data as percentages simplifies the interpretation of complex figures, making it easier to understand and analyze trends.
- Calculate discounts and increases: Percentages are crucial in calculating discounts, sales tax, interest rates, and other financial calculations.
- Express probability and uncertainty: In statistics and probability, percentages are used to express the likelihood of an event occurring.
Calculating 4 Percent of 200: The Methods
There are several ways to calculate 4% of 200. Let's explore the most common approaches:
Method 1: Using the Fraction Method
The percentage can be expressed as a fraction. 4% can be written as 4/100. To find 4% of 200, we multiply 200 by the fraction 4/100:
(4/100) * 200 = 8
Therefore, 4% of 200 is 8.
Method 2: Using the Decimal Method
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. So, 4% becomes 0.04 (4 divided by 100). To find 4% of 200, we multiply 200 by 0.04:
200 * 0.04 = 8
Again, we find that 4% of 200 is 8.
Method 3: Using the Proportion Method
This method involves setting up a proportion. We know that 4% is equivalent to 4 out of 100. We can set up the following proportion:
4/100 = x/200
To solve for x (which represents 4% of 200), we cross-multiply:
100x = 4 * 200 100x = 800 x = 800 / 100 x = 8
This method confirms that 4% of 200 is 8.
Real-World Applications of Percentage Calculations
The ability to calculate percentages has countless real-world applications. Here are a few examples:
1. Financial Calculations:
- Interest calculations: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations is crucial for managing personal finances effectively. For instance, calculating the interest accrued on a savings account or determining the monthly payment on a loan.
- Investment returns: Investors use percentages to track the performance of their investments. Calculating the percentage return on an investment helps in assessing its profitability.
- Sales tax: Sales tax is calculated as a percentage of the purchase price. Understanding this calculation is essential for budgeting and managing expenses.
- Discounts: Retailers often offer discounts as percentages off the original price. Knowing how to calculate these discounts helps consumers make informed purchasing decisions.
2. Business and Sales:
- Profit margins: Businesses calculate their profit margins as a percentage of their revenue to determine profitability.
- Sales growth: Businesses track their sales growth as a percentage to assess their performance over time.
- Market share: Companies use percentages to express their market share, indicating their dominance within a particular industry.
- Commission calculations: Sales representatives often earn commissions based on a percentage of their sales. Calculating these commissions is crucial for their compensation.
3. Statistics and Data Analysis:
- Data representation: Percentages are widely used to represent data in charts and graphs, making it easier to visualize and understand trends.
- Statistical analysis: Many statistical analyses rely on percentage calculations to summarize and interpret data. For instance, calculating the percentage of respondents who answered "yes" to a particular question in a survey.
- Probability and risk assessment: Percentages are used to express the probability of events happening, which is critical in risk assessment and decision-making processes.
Beyond the Basics: More Complex Percentage Problems
While calculating 4% of 200 is relatively straightforward, percentage calculations can become more complex. Here are some examples of more advanced scenarios:
- Calculating the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if sales increased from 100 to 120, the percentage increase is calculated as: [(120-100)/100] * 100% = 20%.
- Finding the original value after a percentage increase or decrease: If a value has been increased by a certain percentage and you know the final value, you can work backward to find the original value.
- Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires more complex percentage calculations.
- Solving percentage word problems: Many real-world problems involve translating word problems into mathematical equations involving percentages. Practice and understanding the underlying concepts are key to mastering this.
Mastering Percentage Calculations: Tips and Tricks
To become proficient in percentage calculations, consider these tips:
- Practice regularly: Consistent practice is key to mastering any mathematical skill. Work through various problems, starting with simple ones and gradually progressing to more complex scenarios.
- Understand the concepts: Don't just memorize formulas; understand the underlying concepts of percentages, fractions, and decimals. This will enable you to solve a wider range of problems.
- Use different methods: Try different methods (fraction, decimal, proportion) to solve the same problem. This helps reinforce your understanding and identify the most efficient approach for different situations.
- Utilize online resources: There are numerous online resources, including calculators and tutorials, that can assist you in learning and practicing percentage calculations.
- Break down complex problems: When faced with a complex problem, break it down into smaller, more manageable steps. This makes the problem less daunting and easier to solve.
Conclusion: The Importance of Percentage Calculations in Everyday Life
In conclusion, understanding percentage calculations is a fundamental skill with far-reaching implications in various aspects of life. From managing personal finances to analyzing data and making informed business decisions, the ability to work comfortably with percentages is invaluable. While calculating 4% of 200 may seem like a simple task, it serves as a gateway to understanding the broader applications of percentages and their importance in navigating the complexities of the modern world. By mastering these fundamental concepts and practicing regularly, you will equip yourself with a powerful tool for tackling numerous real-world challenges and opportunities.
Latest Posts
Latest Posts
-
How To Find Weight From Density
May 25, 2025
-
2 Out Of 17 As A Percentage
May 25, 2025
-
8 Billion Divided By 100 Million
May 25, 2025
-
Half Of 7 8 In Fraction
May 25, 2025
-
What Are The Gcf Of 21 And 40
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.