What Is 4 5 Of 30
listenit
May 25, 2025 · 5 min read
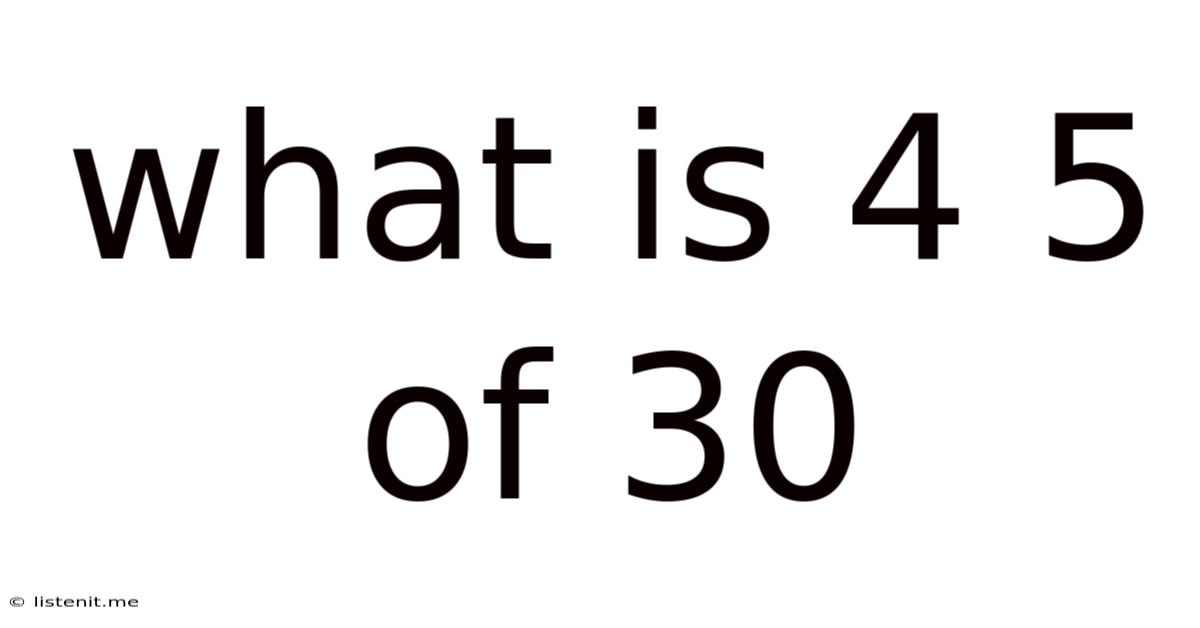
Table of Contents
What is 4/5 of 30? A Deep Dive into Fractions, Percentages, and Real-World Applications
This seemingly simple question, "What is 4/5 of 30?", opens the door to a broader understanding of fractions, percentages, and their practical applications in everyday life. While the answer itself is straightforward, exploring the various methods of solving it and the concepts it encompasses provides valuable insight into mathematical reasoning and problem-solving skills.
Understanding Fractions: The Building Blocks
Before diving into the calculation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating how many parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 4/5, the numerator (4) represents the parts we're interested in, and the denominator (5) represents the total number of equal parts.
Method 1: Direct Multiplication
The most straightforward method to find 4/5 of 30 involves direct multiplication. We can express this mathematically as:
(4/5) * 30
To perform this calculation, we can either multiply the numerator by 30 and then divide by the denominator, or simplify the fraction before multiplying. Let's explore both approaches:
Approach A: Numerator First
- Multiply the numerator by 30: 4 * 30 = 120
- Divide the result by the denominator: 120 / 5 = 24
Approach B: Simplification First
- Simplify the fraction (if possible): In this case, we can't simplify 4/5 further as 4 and 5 share no common factors other than 1.
- Multiply the simplified fraction by 30: (4/5) * 30 = 24
Therefore, 4/5 of 30 is 24.
Method 2: Converting to a Decimal
Another approach involves converting the fraction 4/5 into its decimal equivalent. To do this, we divide the numerator by the denominator:
4 ÷ 5 = 0.8
Now, we can multiply the decimal equivalent by 30:
0.8 * 30 = 24
This method confirms our previous result: 4/5 of 30 is 24.
Method 3: Finding the Value of One-Fifth
This method involves finding the value of one-fifth of 30 and then multiplying by four.
- Divide 30 by 5 (the denominator): 30 / 5 = 6 (This represents one-fifth of 30).
- Multiply the result by 4 (the numerator): 6 * 4 = 24
Again, we arrive at the same answer: 4/5 of 30 is 24.
Connecting Fractions and Percentages
Fractions and percentages are closely related. Percentages represent fractions with a denominator of 100. To express 4/5 as a percentage, we convert it to an equivalent fraction with a denominator of 100:
- Find an equivalent fraction: To get from 5 to 100, we multiply by 20. We must do the same to the numerator: 4 * 20 = 80. This gives us 80/100.
- Convert to a percentage: 80/100 = 80%
Now, we can find 80% of 30:
0.80 * 30 = 24
This demonstrates the equivalence between fractions and percentages in solving this problem.
Real-World Applications: Where Fractions Matter
The concept of finding a fraction of a quantity is prevalent in numerous everyday situations. Here are a few examples:
- Shopping: Calculating discounts. If a store offers a 20% discount on a $50 item, you're essentially finding 80% (100% - 20%) of $50.
- Cooking: Adjusting recipes. If a recipe calls for 2/3 cup of flour but you only want to make half the recipe, you would need to find 1/2 of 2/3 cup.
- Finance: Calculating interest. Compound interest calculations involve finding a fraction of a principal amount repeatedly.
- Construction and Engineering: Determining material quantities. Precise measurements are crucial, often requiring calculations with fractions and decimals to ensure accuracy.
- Data Analysis: Interpreting proportions and percentages in datasets. Understanding fractions is essential for analyzing data and drawing meaningful conclusions.
Beyond the Basics: Expanding Mathematical Skills
While the problem "What is 4/5 of 30?" might seem elementary, mastering the underlying concepts lays a solid foundation for more complex mathematical problems. Understanding fractions, decimals, and percentages is crucial for:
- Algebra: Solving equations involving fractions and variables.
- Geometry: Calculating areas and volumes using fractional dimensions.
- Calculus: Dealing with derivatives and integrals, often involving fractional exponents.
- Statistics: Analyzing data and probability, using proportions and percentages extensively.
Problem-Solving Strategies: A Broader Perspective
The ability to solve "What is 4/5 of 30?" extends beyond the simple arithmetic. It exemplifies a broader problem-solving approach:
- Understanding the Problem: Clearly identifying what is being asked.
- Choosing the Right Method: Selecting the most efficient and appropriate approach.
- Applying Mathematical Concepts: Utilizing relevant knowledge of fractions, decimals, and percentages.
- Checking the Answer: Ensuring the solution is reasonable and accurate.
- Connecting to Real-World Applications: Understanding the relevance of the problem and its practical applications.
By exploring various solution methods and understanding the underlying concepts, we can move beyond a simple arithmetic calculation and develop a deeper appreciation for the power and versatility of fractions in mathematics and everyday life. The seemingly insignificant question, "What is 4/5 of 30?", serves as a gateway to a more profound understanding of mathematical principles and their practical significance. It highlights the interconnectedness of seemingly disparate mathematical concepts, illustrating how a strong foundation in basic arithmetic is crucial for success in more advanced mathematical pursuits. The ability to confidently and accurately solve such problems is a valuable skill that transcends the classroom and applies to numerous aspects of daily life, fostering problem-solving skills that are applicable across a broad spectrum of fields and endeavors.
Latest Posts
Latest Posts
-
421 Divided By 27 With Remainder
May 25, 2025
-
You Re Compatible With 0 Of The Female Population Test
May 25, 2025
-
What Is The Greatest Common Factor Of 26 And 52
May 25, 2025
-
What Percent Of 25 Is 3
May 25, 2025
-
How Do I Measure My Roof
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 5 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.