What Is 36 Divided By 3/4
listenit
May 23, 2025 · 5 min read
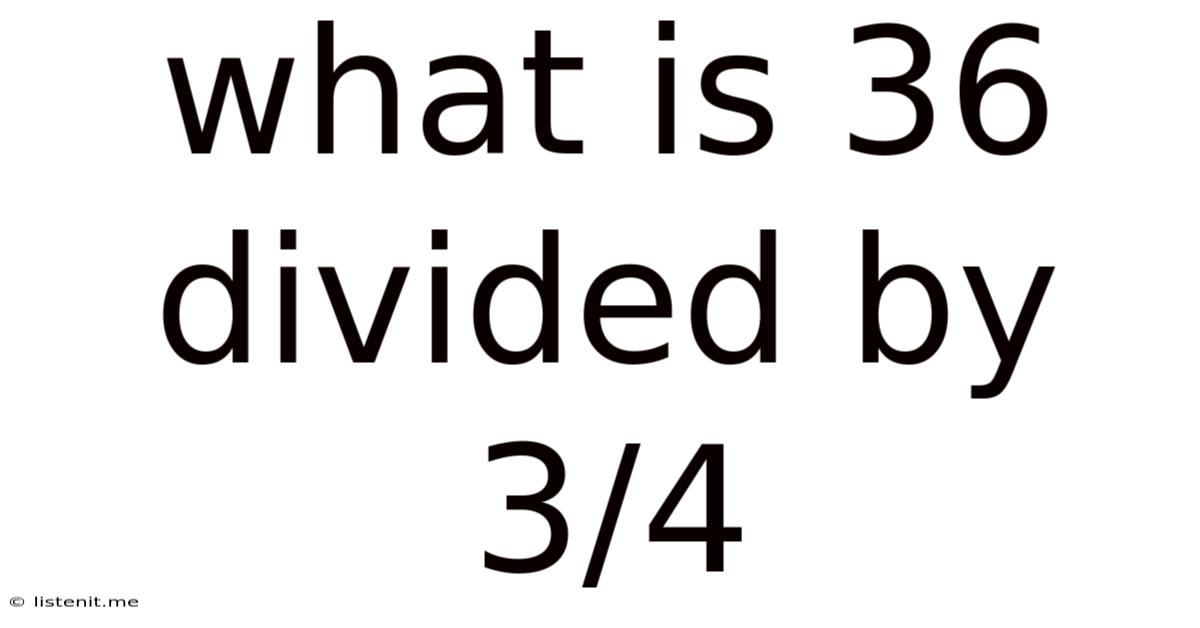
Table of Contents
What is 36 Divided by 3/4? A Deep Dive into Fraction Division
The seemingly simple question, "What is 36 divided by 3/4?" can open a door to a deeper understanding of fraction division. While the answer itself is straightforward once you grasp the mechanics, the underlying principles are crucial for mastering more complex mathematical concepts. This article will not only provide the solution but also explore the "why" behind the process, offering multiple approaches to solving this problem and similar ones, reinforcing your understanding of fractions and division.
Understanding the Problem: 36 ÷ (3/4)
Before diving into the calculation, let's break down the problem. We're asked to divide the whole number 36 by the fraction 3/4. This translates to finding out how many times 3/4 fits into 36. This seemingly simple question often trips up students because it involves dividing by a fraction, a concept that requires a slightly different approach than dividing by a whole number.
Method 1: The "Invert and Multiply" Method
This is the most common method taught for dividing fractions. The rule is simple: to divide by a fraction, you invert (flip) the fraction and then multiply.
Step 1: Invert the Fraction
The fraction 3/4 is inverted to become 4/3.
Step 2: Multiply
Now, we multiply 36 by the inverted fraction:
36 × (4/3) = (36 × 4) / 3 = 144 / 3 = 48
Therefore, 36 divided by 3/4 is 48.
This method is efficient and widely used, but understanding why it works is key to truly mastering fraction division.
Method 2: Visualizing the Division
Imagine you have 36 pizzas. You want to divide these pizzas into servings of 3/4 of a pizza each. How many servings do you have?
To solve this visually, you can think about it in terms of quarters. Each pizza has four quarters (4/4). So, 36 pizzas have 36 x 4 = 144 quarters.
Since each serving is 3 quarters (3/4), you can find the number of servings by dividing the total number of quarters by the number of quarters per serving:
144 quarters ÷ 3 quarters/serving = 48 servings
This visual representation provides a concrete understanding of the process, reinforcing the concept of dividing by a fraction.
Method 3: Converting to Improper Fractions
Another approach involves converting the whole number into a fraction and then applying the standard fraction division rule.
Step 1: Convert the Whole Number to a Fraction
The whole number 36 can be expressed as the fraction 36/1.
Step 2: Divide the Fractions
Now, we divide the fractions:
(36/1) ÷ (3/4) = (36/1) × (4/3) = (36 × 4) / (1 × 3) = 144 / 3 = 48
This method demonstrates the equivalence of whole numbers and fractions with a denominator of 1, further reinforcing the concept of fraction manipulation.
Why Does "Invert and Multiply" Work?
The "invert and multiply" method isn't a magical trick; it's a consequence of the properties of fractions and reciprocals. The reciprocal of a fraction is simply the fraction inverted. Multiplying a number by its reciprocal always results in 1.
Consider this: (a/b) ÷ (c/d) = (a/b) × (d/c)
Let's break it down:
We can rewrite the division problem as a complex fraction:
[(a/b) / (c/d)]
To simplify this complex fraction, we multiply both the numerator and denominator by the reciprocal of the denominator (d/c):
[(a/b) × (d/c)] / [(c/d) × (d/c)] = [(a/b) × (d/c)] / 1 = (a/b) × (d/c)
This shows that dividing by a fraction is equivalent to multiplying by its reciprocal. This understanding solidifies the "invert and multiply" method and explains its effectiveness.
Practical Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in everyday life and various professions:
-
Cooking and Baking: Scaling recipes up or down requires dividing and multiplying fractions. If a recipe calls for 1/2 cup of flour and you want to make three times the recipe, you'll need to calculate 3 x (1/2).
-
Sewing and Crafting: Cutting fabric or other materials often involves fractions of inches or centimeters. Dividing lengths accurately ensures precise cuts.
-
Construction and Engineering: Accurate measurements and calculations in construction and engineering often rely on understanding fractions and their manipulation. Dividing lengths, areas, or volumes according to specifications is crucial.
-
Financial Calculations: Dividing shares of stock, calculating interest rates, or splitting bills amongst a group of people often involves fractions and their division.
-
Data Analysis: In statistical analysis, manipulating data often requires dividing and manipulating fractions and decimals for accurate analysis and interpretation of results.
Expanding Your Knowledge: Beyond Simple Fractions
While this article focuses on dividing a whole number by a simple fraction, the principles discussed apply to dividing any number (whole number, fraction, decimal) by any fraction. The key is to master the core concepts of fraction division, including the "invert and multiply" method and its underlying rationale. With practice, you'll be able to tackle more complex fraction division problems with confidence.
Further Exploration: Mixed Numbers and Decimals
This article focused on dividing a whole number by a simple fraction. However, you can apply the same principles to problems involving mixed numbers (numbers with both whole and fractional parts) and decimals. To divide with mixed numbers, convert them into improper fractions first, and then apply the "invert and multiply" method. For decimals, converting them into fractions is a useful approach.
Conclusion: Mastering Fraction Division
Understanding "What is 36 divided by 3/4?" is not just about getting the answer (48). It’s about gaining a solid grasp of fraction division principles. By exploring different methods and understanding the underlying rationale, you'll not only solve this specific problem but build a strong foundation for more complex mathematical challenges in various fields. Remember the power of visualization and the fundamental rule of "invert and multiply" – these are your keys to unlocking the world of fraction division. The more you practice, the more comfortable and confident you'll become in handling these types of calculations.
Latest Posts
Latest Posts
-
How Fast Is 8 Miles A Minute
May 24, 2025
-
25 Is What Percentage Of 100
May 24, 2025
-
If You Are Born In 1980 How Old Are You
May 24, 2025
-
What Percent Is 6 Of 16
May 24, 2025
-
What Is 14 As A Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 36 Divided By 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.