What Is 3 5 Of 20
listenit
May 21, 2025 · 5 min read
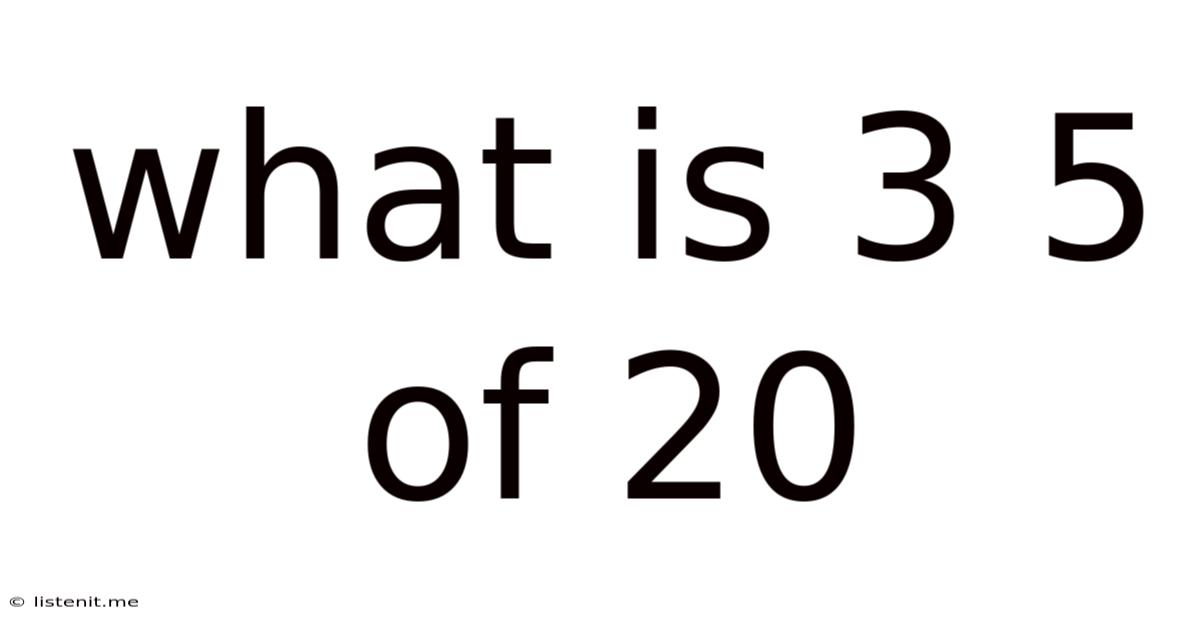
Table of Contents
What is 3/5 of 20? A Comprehensive Guide to Fractions and Percentages
Finding a fraction of a number is a fundamental mathematical concept with wide-ranging applications in everyday life, from calculating discounts and tips to understanding proportions in recipes and scaling projects. This article will delve into the question, "What is 3/5 of 20?", exploring the various methods for solving this problem and providing a deeper understanding of fractions, percentages, and their practical uses. We'll also discuss some common mistakes to avoid and offer additional exercises to solidify your understanding.
Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In the fraction 3/5, 3 is the numerator and 5 is the denominator.
Key Concepts Related to Fractions:
- Equivalent Fractions: These are fractions that represent the same value, even though they look different. For instance, 1/2, 2/4, and 3/6 are all equivalent fractions.
- Simplifying Fractions: This involves reducing a fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 6/9 can be simplified to 2/3 by dividing both by 3.
- Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾). You can convert between the two.
- Adding, Subtracting, Multiplying, and Dividing Fractions: These operations require understanding common denominators (for addition and subtraction) and the rules for multiplying and dividing numerators and denominators.
Calculating 3/5 of 20: Three Approaches
There are several ways to calculate 3/5 of 20. Let's explore three common methods:
Method 1: Multiplication
The most straightforward method involves multiplying the fraction by the whole number:
(3/5) * 20
To perform this multiplication, we can rewrite 20 as a fraction (20/1):
(3/5) * (20/1) = (3 * 20) / (5 * 1) = 60 / 5
Now, we simplify the fraction by dividing the numerator by the denominator:
60 / 5 = 12
Therefore, 3/5 of 20 is 12.
Method 2: Finding One-Fifth, Then Multiplying
This method involves first finding what one-fifth (1/5) of 20 is, and then multiplying that result by 3.
- Find one-fifth: Divide 20 by 5: 20 / 5 = 4. One-fifth of 20 is 4.
- Multiply by three: Since we want three-fifths, we multiply the result from step 1 by 3: 4 * 3 = 12.
Again, we find that 3/5 of 20 is 12.
Method 3: Using Decimals
We can convert the fraction 3/5 into a decimal by dividing the numerator by the denominator:
3 / 5 = 0.6
Then, multiply the decimal by 20:
0.6 * 20 = 12
This method provides the same answer: 3/5 of 20 is 12.
Practical Applications and Real-World Examples
Understanding how to calculate fractions of numbers is crucial in numerous real-world scenarios:
- Shopping Discounts: If a store offers a 3/5 discount on an item priced at $20, you would save (3/5) * $20 = $12.
- Recipe Scaling: If a recipe calls for 3/5 of a cup of flour, and you want to double the recipe, you'll need 2 * (3/5) = 6/5 or 1 1/5 cups of flour.
- Project Management: If a project is estimated to take 20 days, and 3/5 of it is complete, then 12 days of work have been finished.
- Financial Calculations: Determining portions of investments, calculating interest, or splitting bills are all situations that require fraction calculations.
- Data Analysis: Many statistical calculations rely heavily on fractions and ratios to understand proportions and trends within datasets.
Common Mistakes to Avoid
Several common pitfalls can lead to incorrect answers when calculating fractions:
- Incorrect Order of Operations: Remember that multiplication and division should be performed before addition and subtraction.
- Errors in Simplification: Always simplify fractions to their lowest terms for accuracy and clarity.
- Misinterpreting the Problem: Carefully read the problem statement to ensure you understand what is being asked.
- Incorrect Decimal Conversion: When converting fractions to decimals, ensure the division is performed correctly.
- Forgetting to Multiply After Finding One-Fifth (or Other Unit Fraction): This is a common error in Method 2.
Further Practice Exercises
To solidify your understanding, try solving these problems:
- What is 2/3 of 15?
- What is 5/8 of 24?
- What is 7/10 of 50?
- A shirt is discounted by 2/5 of its original price of $30. What is the discounted price?
- A recipe calls for 1/4 of a cup of sugar. How much sugar is needed if you triple the recipe?
These exercises will help you practice applying the methods discussed and reinforce your understanding of fractions and their applications.
Conclusion: Mastering Fractions for Everyday Success
The ability to accurately calculate fractions is an essential life skill with broad applications across many fields. By understanding the underlying principles and practicing various methods, you can confidently tackle fraction problems and apply this knowledge to various real-world situations. Remember to avoid common mistakes and practice regularly to improve your proficiency. This foundational understanding will significantly contribute to your success in various academic and practical contexts. Mastering fractions isn't just about solving math problems; it's about developing a crucial skillset for problem-solving in everyday life.
Latest Posts
Latest Posts
-
What Is The Main Goal Of Long Term Care
Jun 05, 2025
-
What Is The Key Characteristic Of A Transformed Cell
Jun 05, 2025
-
Primary Care Versus Primary Health Care
Jun 05, 2025
-
The Evolution Of Eukaryotic Cells Most Likely Involved
Jun 05, 2025
-
P Wave Inversion In V1 And V2
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.