What Is 3 5 Of 15
listenit
May 25, 2025 · 5 min read
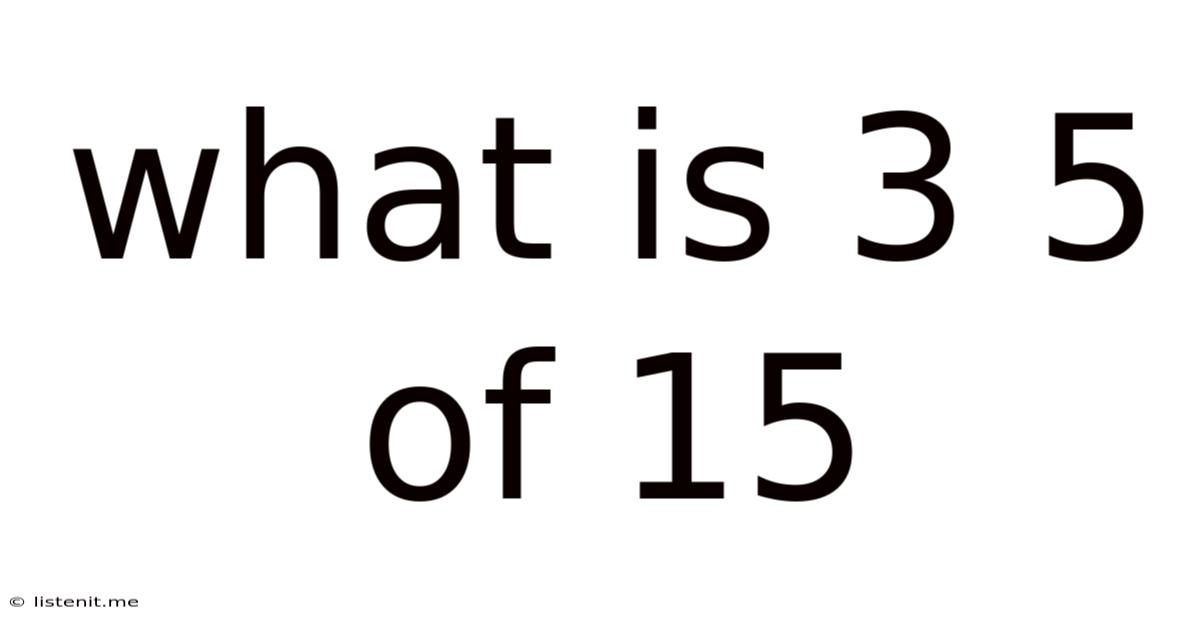
Table of Contents
What is 3/5 of 15? A Comprehensive Guide to Fractions and Percentages
This seemingly simple question, "What is 3/5 of 15?", opens the door to a deeper understanding of fractions, percentages, and their practical applications in everyday life. While the answer itself is straightforward, exploring the various methods of solving it and the underlying mathematical concepts enhances our numerical literacy and problem-solving skills. This article will not only provide the solution but also delve into the 'why' and 'how,' equipping you with the tools to tackle similar problems confidently.
Understanding the Fundamentals: Fractions and Percentages
Before diving into the calculation, let's refresh our understanding of fractions and percentages.
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 3/5, 3 is the numerator and 5 is the denominator. This means we have 3 parts out of a total of 5 parts.
What is a Percentage?
A percentage is a fraction expressed as a part of 100. It represents a proportion out of a hundred. The percentage symbol (%) signifies "per hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Solving "What is 3/5 of 15?" – Three Different Approaches
Now, let's tackle the core question using three distinct methods:
Method 1: Direct Multiplication
This is the most straightforward method. To find 3/5 of 15, we multiply the fraction (3/5) by the whole number (15):
(3/5) * 15 = (3 * 15) / 5 = 45 / 5 = 9
Therefore, 3/5 of 15 is 9.
Method 2: Finding the Unit Fraction
This method involves first finding the value of one-fifth (1/5) of 15 and then multiplying that value by 3.
1/5 of 15 = 15 / 5 = 3
Now, we multiply this value by 3 to find 3/5 of 15:
3 * 3 = 9
Again, we arrive at the answer: 9.
Method 3: Converting to a Decimal
We can convert the fraction 3/5 into a decimal by dividing the numerator (3) by the denominator (5):
3 / 5 = 0.6
Now, we multiply this decimal by 15:
0.6 * 15 = 9
This approach demonstrates the interchangeability between fractions and decimals.
Expanding the Concept: Real-World Applications
The ability to calculate fractions and percentages is crucial in various real-world scenarios:
-
Shopping: Calculating discounts, sales tax, or the final price after a percentage discount. For example, if a shirt costs $15 and is on sale for 3/5 off, you'd save $9 (3/5 of $15).
-
Cooking and Baking: Adjusting recipes based on the number of servings. If a recipe calls for 3/5 of a cup of sugar and you want to double the recipe, you'll need to calculate 2 x (3/5) cups of sugar.
-
Finance: Calculating interest, compound interest, or understanding loan repayments. Interest rates are often expressed as percentages.
-
Data Analysis: Interpreting statistical data often involves working with fractions and percentages. For example, understanding market share or survey results.
-
Construction and Engineering: Precise measurements are crucial, and fractions and decimals are essential in blueprints and calculations.
Advanced Concepts and Extensions
Let's explore more complex scenarios to further solidify our understanding:
Dealing with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 2 1/2). To calculate a fraction of a mixed number, first convert the mixed number into an improper fraction (where the numerator is greater than or equal to the denominator). For example, to find 3/5 of 2 1/2:
-
Convert 2 1/2 to an improper fraction: (2 * 2 + 1) / 2 = 5/2
-
Multiply the fractions: (3/5) * (5/2) = 15/10 = 3/2
-
Convert back to a mixed number if necessary: 3/2 = 1 1/2
Calculating Percentages of a Number
To calculate a percentage of a number, convert the percentage to a decimal and multiply it by the number. For example, to find 60% of 15:
-
Convert 60% to a decimal: 60/100 = 0.6
-
Multiply by 15: 0.6 * 15 = 9
This demonstrates the close relationship between fractions, decimals, and percentages.
Solving Word Problems Involving Fractions and Percentages
Many real-world problems involve fractions and percentages. Carefully read the problem to identify the key information and choose the appropriate method to solve it. For example:
"John has 15 apples. He gives 3/5 of his apples to his friend. How many apples does he have left?"
-
Calculate 3/5 of 15: (3/5) * 15 = 9
-
Subtract the number of apples given away from the original number: 15 - 9 = 6
John has 6 apples left.
Conclusion: Mastering Fractions and Percentages for Everyday Success
Understanding fractions and percentages is fundamental to navigating various aspects of life. This comprehensive guide explored the different ways to calculate 3/5 of 15, highlighting the underlying mathematical concepts and demonstrating their practical applications. By mastering these skills, you'll be better equipped to tackle everyday challenges, make informed decisions, and excel in areas that require numerical fluency. Remember to practice regularly to build confidence and proficiency in working with fractions and percentages. The seemingly simple question, "What is 3/5 of 15?", acts as a springboard to a world of numerical understanding and problem-solving capabilities.
Latest Posts
Latest Posts
-
How Big Is 36 Square Feet In Feet
May 25, 2025
-
Highest Common Factor Of 72 And 96
May 25, 2025
-
Find The Volume Of The Given Figure
May 25, 2025
-
Greatest Common Factor 12 And 48
May 25, 2025
-
How To Divide 7 By 8
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 5 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.