What Is 3 4 Divided By 1 8
listenit
May 24, 2025 · 5 min read
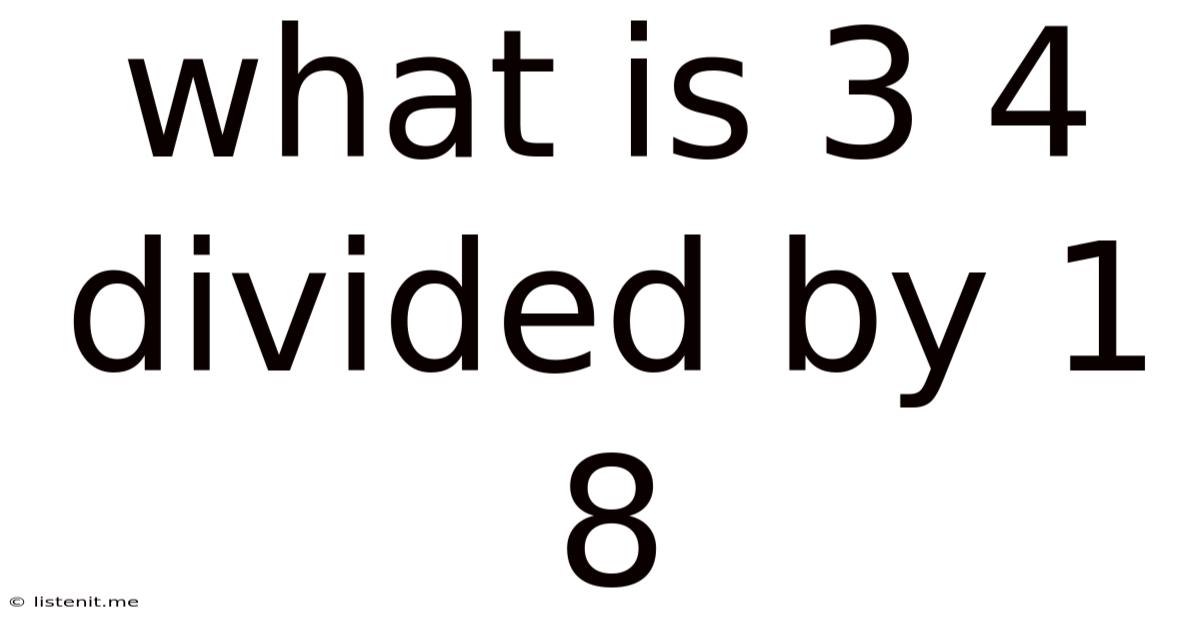
Table of Contents
What is 3/4 Divided by 1/8? A Deep Dive into Fraction Division
This seemingly simple question, "What is 3/4 divided by 1/8?", opens the door to a fascinating exploration of fraction division, a fundamental concept in mathematics with widespread applications in various fields. While the answer itself is straightforward, understanding the underlying principles and different methods for solving such problems is crucial for developing a strong mathematical foundation. This article will delve into the mechanics of fraction division, explore various approaches, and demonstrate its practical relevance.
Understanding Fraction Division: The "Why" Behind the "How"
Before jumping into the calculation, let's grasp the fundamental concept behind dividing fractions. When we divide a number by a fraction, we're essentially asking: "How many times does the second fraction fit into the first fraction?" This perspective helps visualize the operation and understand why the process involves inverting and multiplying.
Imagine you have a pizza cut into four slices. You possess three of those slices (3/4 of the pizza). Now, you want to know how many portions of 1/8 of the pizza you have. This is precisely what 3/4 divided by 1/8 represents. Intuitively, you might expect the answer to be greater than one, as 1/8 is a smaller fraction than 3/4.
Method 1: The "Invert and Multiply" Method – The Standard Approach
This is the most common and efficient method for dividing fractions. The rule is simple: invert (reciprocate) the second fraction (the divisor) and then multiply the two fractions.
In our example:
3/4 ÷ 1/8 = 3/4 x 8/1
Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 x 8) / (4 x 1) = 24/4
Finally, simplify the resulting fraction:
24/4 = 6
Therefore, 3/4 divided by 1/8 equals 6. This means six portions of 1/8 pizza fit into three-quarters of a pizza.
Step-by-Step Breakdown for Beginners:
-
Identify the dividend and divisor: In the problem 3/4 ÷ 1/8, 3/4 is the dividend and 1/8 is the divisor.
-
Invert the divisor: Flip the divisor fraction upside down. 1/8 becomes 8/1.
-
Multiply the fractions: Multiply the dividend by the inverted divisor: (3/4) * (8/1).
-
Simplify: Reduce the resulting fraction to its simplest form.
Method 2: Using Common Denominators – A Visual Approach
While the "invert and multiply" method is efficient, understanding the concept through common denominators offers a visual interpretation. This method is particularly helpful for beginners.
-
Find a common denominator: Find a common denominator for both fractions. In this case, the least common multiple of 4 and 8 is 8.
-
Convert fractions to equivalent fractions: Convert both fractions to equivalent fractions with the common denominator:
3/4 = 6/8 (multiply numerator and denominator by 2) 1/8 = 1/8
-
Divide the numerators: Now, divide the numerators: 6/1 = 6
Therefore, 3/4 divided by 1/8 equals 6. This method provides a clear visual representation of how many times 1/8 fits into 6/8.
Method 3: Converting to Decimal – An Alternative Approach
This method involves converting the fractions to decimals before performing the division. This approach can be beneficial when dealing with more complex fractions or when using a calculator.
-
Convert fractions to decimals:
3/4 = 0.75 1/8 = 0.125
-
Divide the decimals:
0.75 ÷ 0.125 = 6
Therefore, 3/4 divided by 1/8 equals 6. This method offers an alternative way to solve the problem, especially useful when dealing with fractions that are not easily simplified.
Real-World Applications of Fraction Division
The concept of dividing fractions isn't confined to the classroom; it's a practical skill applied in numerous real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'll need to divide 1/2 by 2.
-
Construction and Engineering: Precise measurements are vital, and often involve fractions of inches or meters. Dividing fractions accurately is crucial for accurate calculations.
-
Sewing and Tailoring: Cutting fabric according to precise measurements often necessitates dividing fractions to determine the correct lengths.
-
Finance and Budgeting: Allocating funds or calculating proportions of a budget often involves dividing fractions to understand the breakdown of resources.
-
Data Analysis: Many statistical analyses involve fractions and proportions, requiring division of fractions to understand relationships between datasets.
Advanced Concepts and Further Exploration
While this article focused on the basics of dividing fractions, there are more advanced concepts to explore:
-
Dividing mixed numbers: Mixed numbers (e.g., 1 1/2) require conversion to improper fractions before applying the division rules.
-
Dividing fractions with variables: Algebra introduces the concept of dividing algebraic fractions, requiring similar principles but with variables involved.
-
Complex fractions: These involve fractions within fractions, demanding a multi-step approach involving simplifying the numerator and denominator separately before division.
-
Applications in Calculus: Understanding fraction division lays the groundwork for understanding derivatives and integrals in calculus.
Conclusion: Mastering the Art of Fraction Division
Mastering fraction division is essential for anyone pursuing a strong mathematical foundation. While the "invert and multiply" method offers efficiency, understanding the concept through common denominators or decimal conversion provides a deeper understanding of the underlying principles. Remember that this fundamental skill extends far beyond the classroom, finding its application in numerous real-world situations, highlighting its importance in various fields. Continued practice and exploration of advanced concepts will solidify your understanding and prepare you for more complex mathematical challenges. The journey into the world of fractions is rewarding, and the ability to confidently divide them opens doors to a wider range of mathematical possibilities.
Latest Posts
Latest Posts
-
How Many Hours Is 11am To 10pm
May 24, 2025
-
What Day Of The Week Is March 5th
May 24, 2025
-
Rounding 7 To The Nearest Ten
May 24, 2025
-
What Day Will It Be Tomorrow
May 24, 2025
-
Confidence Interval For The Population Variance Calculator
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Divided By 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.