What Is 3/4 Divided By 1/4
listenit
May 21, 2025 · 5 min read
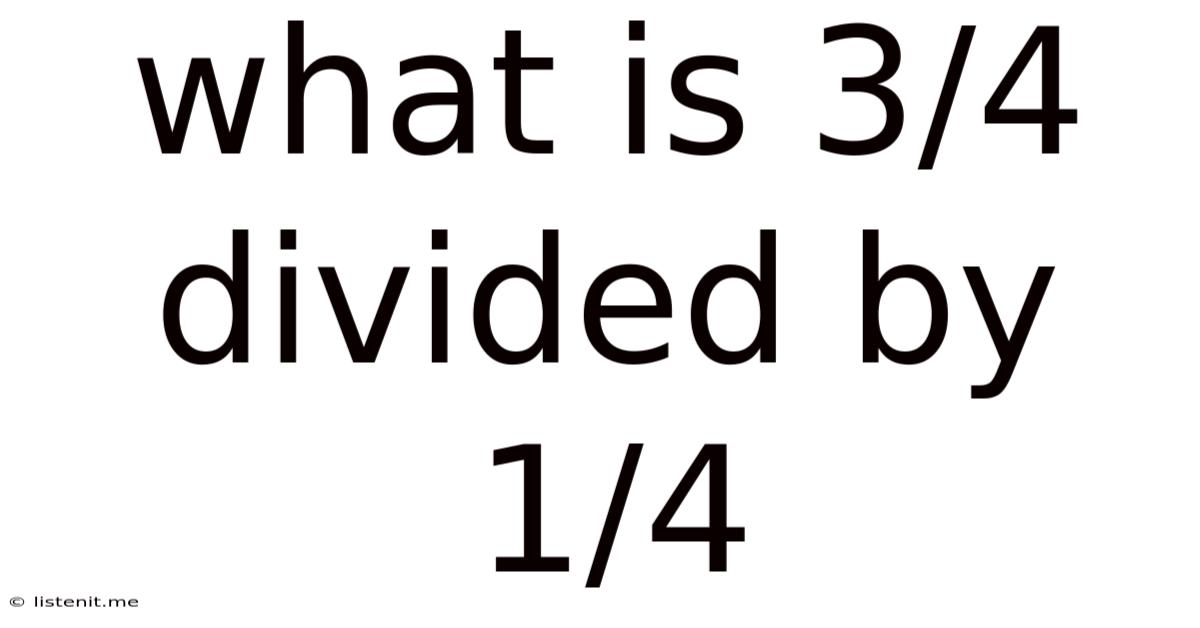
Table of Contents
What is 3/4 Divided by 1/4? A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will not only answer the question, "What is 3/4 divided by 1/4?", but also provide a comprehensive explanation of fraction division, including various methods and practical examples. We'll explore the underlying principles and build your confidence in tackling similar problems. Let's dive in!
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common and arguably easiest method for dividing fractions is the "keep, change, flip" method. This method involves three simple steps:
- Keep: Keep the first fraction exactly as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip the second fraction (reciprocal). This means swapping the numerator and the denominator.
Let's apply this to our problem: 3/4 divided by 1/4.
- Keep: 3/4
- Change: ÷ becomes ×
- Flip: 1/4 becomes 4/1
This transforms the problem from 3/4 ÷ 1/4 to 3/4 × 4/1.
Multiplying the Fractions
Now that we've transformed the division problem into a multiplication problem, we can simply multiply the numerators together and the denominators together:
(3 × 4) / (4 × 1) = 12/4
Simplifying the Result
The result, 12/4, is an improper fraction (the numerator is larger than the denominator). We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4 in this case:
12/4 = 3
Therefore, 3/4 divided by 1/4 equals 3.
Visualizing the Division: A Real-World Analogy
Imagine you have a pizza cut into four equal slices. You have three of those slices (3/4 of the pizza). You want to know how many 1/4 slices are in your 3/4 portion. Visually, it's easy to see that there are three 1/4 slices in your 3/4 portion. This visual representation reinforces the answer we obtained through calculation.
Alternative Methods for Dividing Fractions
While the "keep, change, flip" method is widely used and efficient, there are alternative approaches to dividing fractions. Understanding these alternative methods provides a deeper understanding of the underlying mathematical principles.
Method 1: Using the Reciprocal
The "keep, change, flip" method essentially utilizes the concept of reciprocals. The reciprocal of a fraction is obtained by switching its numerator and denominator. Dividing by a fraction is the same as multiplying by its reciprocal.
Therefore, 3/4 ÷ 1/4 = 3/4 × 4/1 = 3
Method 2: Converting to Decimal Numbers
You can also convert the fractions to decimal numbers before performing the division.
3/4 = 0.75 1/4 = 0.25
0.75 ÷ 0.25 = 3
While this method works, it's often less efficient than the "keep, change, flip" method, especially when dealing with more complex fractions. It also introduces the potential for rounding errors.
Expanding the Understanding: More Complex Fraction Division
Let's explore some more complex examples to solidify your understanding of fraction division.
Example 1: 5/6 ÷ 2/3
- Keep: 5/6
- Change: ÷ becomes ×
- Flip: 2/3 becomes 3/2
(5/6) × (3/2) = (5 × 3) / (6 × 2) = 15/12
Simplifying: 15/12 = 5/4 or 1 1/4
Example 2: 2 1/2 ÷ 1/4
First, convert the mixed number (2 1/2) into an improper fraction: (2 × 2 + 1)/2 = 5/2
- Keep: 5/2
- Change: ÷ becomes ×
- Flip: 1/4 becomes 4/1
(5/2) × (4/1) = (5 × 4) / (2 × 1) = 20/2 = 10
Example 3: 1/3 ÷ 2/5
- Keep: 1/3
- Change: ÷ becomes ×
- Flip: 2/5 becomes 5/2
(1/3) × (5/2) = 5/6
Practical Applications of Fraction Division
Fraction division isn't just a theoretical concept; it has numerous practical applications in everyday life and various fields:
- Cooking and Baking: Adjusting recipes, scaling up or down ingredient quantities.
- Sewing and Crafting: Calculating fabric requirements, dividing patterns.
- Construction and Engineering: Measuring and cutting materials, calculating proportions.
- Finance: Dividing shares, calculating portions of investments.
- Data Analysis: Working with proportions and percentages.
Troubleshooting Common Mistakes in Fraction Division
While the "keep, change, flip" method is relatively straightforward, some common mistakes can occur:
- Forgetting to flip the second fraction: This leads to an incorrect multiplication and, ultimately, an inaccurate answer.
- Incorrectly simplifying fractions: Always ensure that you simplify the final fraction to its lowest terms.
- Mixing up numerators and denominators when flipping: Pay close attention to which number is the numerator and which is the denominator.
- Not converting mixed numbers to improper fractions before dividing: Remember to convert mixed numbers to improper fractions before applying the "keep, change, flip" method.
Conclusion: Mastering Fraction Division
Dividing fractions is a fundamental skill with far-reaching applications. By understanding the "keep, change, flip" method, along with alternative approaches and common pitfalls, you can confidently tackle fraction division problems and apply this knowledge to solve real-world problems. Remember to practice regularly to solidify your understanding and build your fluency. The more you practice, the easier it will become. Now you're equipped to not only answer "What is 3/4 divided by 1/4?" but also handle a wide range of fraction division problems with ease and confidence.
Latest Posts
Latest Posts
-
Selective Caries Removal With A Pulp Cap
Jun 05, 2025
-
Upper Pole Of Kidney On Ultrasound
Jun 05, 2025
-
Giant Cell Tumor Of Bone Histology
Jun 05, 2025
-
Basal Cell Chicken Pox Scar Leg
Jun 05, 2025
-
Lip Lowering Surgery For Gummy Smile
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 Divided By 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.